Líneas de Investigación:

• Relatividad General Clásica y Cuántica.
• Cosmología Cuántica de Lazos.
• Teoría Cuántica de Campos en Espaciotiempos Curvos.
• Gravedad cuántica no-local.
• Espaciotiempos multiescala.
• Ondas gravitacionales (Consorcio LISA).

Labor Investigadora

El Grupo de Gravitación y Cosmología ha continuado su investigación en Cosmología Cuántica de Lazos y su aplicación al Universo primitivo, investigando las consecuencias sobre las perturbaciones cosmológicas. Las perturbaciones estudiadas no son solo perturbaciones de la geometría, sino también de campos escalares (que conducen a perturbaciones primordiales escalares y tensoriales) y de campos fermiónicos.

Durante este año, gran parte del trabajo se ha dedicado a la consideración de una regularización alternativa de la ligadura hamiltoniana de la Cosmología Cuántica de Lazos, diferente a la que se propuso originalmente en la literatura. Esta alternativa se denomina con frecuencia como regularización de Dapor-Liegener para la Cosmología Cuántica de Lazos. En años pasados, ya habíamos discutido su implementación en una cosmología homogénea e isótropa, obteniendo una descripción cuántica de un Universo como el nuestro en promedio. En 2020 hemos ampliado este estudio a cosmologías homogéneas y anisótropas y, además, a cosmologías perturbadas que contienen pequeñas anisotropías e inhomogeneidades. Usando el formalismo de cuantización híbrida en el marco de la Cosmología Cuántica de Lazos, formalismo que fue introducido hace unos diez años por nuestro grupo, hemos obtenido las ecuaciones dinámicas que gobiernan la propagación de las perturbaciones cosmológicas en el Universo primordial, que contienen correcciones cuánticas que son importantes en épocas remotas cercanas a lo que clásicamente llamaríamos el Big Bang. Estas ecuaciones dinámicas son similares a las ecuaciones encontradas en la Relatividad General, pero la masa efectiva dependiente del tiempo que sienten las perturbaciones difiere del resultado de la teoría einsteiniana cuando los efectos de la geometría cuántica son importantes. Hemos analizado el comportamiento de esta masa efectiva, en particular alrededor del rebote que reemplaza al Big Bang en la Cosmología Cuántica de Lazos. Hemos demostrado que esta masa tiene un buen comportamiento en el formalismo híbrido para la cuantización, mientras que este no es el caso en otros formalismos (como, por ejemplo, el llamado formalismo de métrica vestida). Estos resultados permiten un tratamiento detallado de las perturbaciones primordiales con garantías de éxito en la cuantización de Loops con la nueva regularización, incluido el cálculo de los espectros de potencia para las perturbaciones, que podrían compararse con observaciones.

Otra parte importante de nuestro trabajo se ha centrado en la discusión de perturbaciones fermiónicas correspondientes a un campo de Dirac. En particular, hemos mostrado cómo el criterio de diagonalización hamiltoniana asintótica, originado en la Cosmología Cuántica de Lazos híbrida, sirve para seleccionar un vacío único para el campo de Dirac en las cosmologías de tipo de Sitter, en el contexto de teoría cuántica de campos en espaciotiempos curvos. El criterio empleado se basa en alcanzar una definición dinámica adecuada de las variables de creación y destrucción para el campo fermiónico, con un hamiltoniano asociado que resulte ser asintóticamente diagonal. Esto conduce a variables fermiónicas que poseen una expansión asintótica precisa en el límite ultravioleta de grandes números de onda. Hemos demostrado que, cuando el fondo cosmológico se fija como una solución de Sitter, esta expansión determina completamente la elección de las variables de creación y destrucción fermiónicas para todas las escalas espaciales, y por lo tanto selecciona una representación de Fock privilegiada y un estado de vacío para el campo de Dirac.

También hemos investigado la producción gravitatoria de materia oscura acoplada a la curvatura durante las épocas inflacionaria y de recalentamiento. Hemos desarrollado una aproximación analítica para describir el efecto relevante de resonancia y sus consecuencias en el régimen ultravioleta permitiéndonos así constreñir los posibles valores de los valores fenomenológicos del campo que estamos considerando como candidato a materia oscura.

Hemos investigado los efectos de la polarización del vacío es espaciotiempos esféricamente simétricos, estáticos y vacíos. Comenzamos con la aproximación de Polyakov para el tensor de energía-momento renormalizado y encontramos todas las soluciones a las ecuaciones del campo semiclásicas en vacío. La contrapartida a la geometría clásica de Schwarzschild reemplaza la presencia de un horizonte de sucesos por la garganta de un agujero de gusano que conecta una región externa asintóticamente plana con una región asintótica interna que posee una singularidad desnuda: no hay ninguna solución semiclásica de vacío con superficies de Cauchy. Hemos analizado espaciotiempos asintóticamente planos y esféricamente simétricos en los que aparece un horizonte de sucesos sin superficies atrapadas encontrando dos tipos diferentes, cada uno de ellos relacionado con el comportamiento de uno de los dos grados de libertad de la métrica. El resultado es que casi siempre aparece un horizonte de Cauchy más allá del cual se puede extender la métrica, mientras que el otro es inextensible pero tiene dos regiones asintóticas futuras nulas a cada lado del horizonte. También hemos estudiado las condiciones de energía que debe satisface la materia en las proximidades del horizonte.

Hemos analizado la cuantización de un campo escalar en presencia de un campo electromagnético clásico externo y hemos encontrado una representación de natural de Fock que admite una implementación unitaria de la dinámica del campo cuántico. Permite definir automáticamente una densidad de partículas en cualquier momento de la evolución con el comportamiento asintótico correcto. También hemos demostrado la equivalencia unitaria de todas las cuantizaciones que satisfacen estos criterios. Aunque hemos llevado a cabo la cuantización en un gauge específico, los procedimientos llevados a cabo en diferentes gauges son equivalentes.

Con respecto a las ondas gravitacionales, nuestra activitdad se ha centrado principalmente en proyectos definitorios de la ciencia de LISA. Por un lado, hemos publicado el “manifesto” del Fundamental Physics Working Group, donde hemos establecido nuestra visión de qué señales de física más allá de la relatividad general buscar con este experimento, qué modelos y teorías privilegiar en dicha búsqueda y qué características explorar más en detalle: relaciones de dispersión modificadas, violaciones del principio de equivalencia y de la simetrías fundamentales, modelos de energía oscura, de materia oscura y de agujeros negros, entre otras. En el curso del año hemos estado preparando también el Artículo Blanco del Cosmology Working Group, todavía en fase de escritura. Estamos coordinando la sección del fondo estocásticos de ondas gravitacionales, dentro de las tareas requeridas para los miembros plenos del Consorcio, categoría en la que hemos pasado en 2020.

Relacionado con estos temas, pero desarrollado fuera del Consorcio, señalamos un artículo sobre el fondo estocástico de ondas gravitacionales en gravedad cuántica, proyecto que ha requerido varios meses de desarrollo. Hemos explorado por primera vez la producción de un fondo estocástico en un catálogo de numerosos modelos cosmológicos procedentes de teorías de gravedad cuántica y establecido qué modelos pueden producir un espectro azul en las frecuencias de los interferómetros actuales y futuros. La cosmología de gas de cuerdas, el nuevo escenario ekpyrótico, la inflación no-conmutativa de Brandenberger y Ho y los espaciotiempos multi-escala pueden producir una señal detectable por DECIGO, y en el caso del nuevo escenario ekpyrótico, también por el Einstein Telescope, misión en que el IEM tiene una participación. Sin embargo, ninguno de ellos llega a la curva de sensitividad de LISA o de la red LIGO-Virgo-KAGRA. Contrariamente a lo esperado en la literatura, la gravedad cuántica no-local, una de las principales teorías bajo el foco investigador del grupo, no produce un fondo estocástico de ondas gravitacionales detectable. Es es debido al hecho de que a altas frecuencias el espectro tiende al predicho por el modelo de inflación de Starobinsky, cuya amplitud está muy por debajo de las curvas de sensitividad de los experimentos. Estos y otros resultados han sido resumidos en el capítulo de un manual de Astronomía de Ondas Gravitacionales de tres volúmenes que será publicado por Springer en 2021.

El hito principal alcanzado respecto al estudio de teorías multi-escala ha sido la verificación de la posibilidad de generar una aceleración cósmica tardía en una de las cuatro teorías desarrolladas por el grupo a partir de 2010. En esta teoría, la energía oscura se interpreta como un fenómeno derivado de una expansión no-estándar guiada ni por un campo escalar ni por efectos de curvatura, sino por la estructura multi-fractal de la geometría del espaciotiempo, realizada por un cálculo integrodiferencial específico para sistemas multi-escala y fractales. Esta explicación resulta natural en el sentido de que no hay ajustes finos en los parámetros de la teoría.

También subrayamos nuestra participación en la coordinación y escritura del Volumen 9 del Libro Blanco del CSIC, publicado por la Editorial CSIC en una colaboración a nivel nacional con todos los grupos principales de física teórica, astrofísica y cosmología del Consejo. En particular, hemos contribuido a la redacción del capítulo 4 “Origin and Fate of the Universe” sobre inflación, bariogénesis, materia oscura, energía oscura y ondas gravitacionales, y a la coordinación y redacción del capítulo 7 “Gravity” sobre modelos de gravedad cuántica y de altas energías aplicados a la cosmología y a fenómenos gravitatorios en general.

Algunos de los temas de investigación de nuestro grupo en física gravitacional hacen uso de técnicas matemáticas en las que la combinatoria y la teoría de números juegan un papel esencial. Por ejemplo, los estudios realizados por algunos miembros del grupo sobre el espectro del operador de área se basan en el uso de la teoría analítica de números. En el curso de estas investigaciones ha sido necesario obtener y caracterizar algunas nuevas identidades para los números de Bernoulli. En primer lugar, conjeturamos estas identidades tras identificarlas con la ayuda de programas de cálculo simbólica y la OEIS (enciclopedia en línea de secuencias enteras) y luego las demostramos (Comptes Rendus. Mathèmatique, 357 (2020) 1, 41-44). De manera similar, hemos aplicado nuestros conocimientos sobre métodos asintóticos en teoría analítica de números (que adquirimos en el curso del trabajo sobre la entropía del agujero negro que llevamos a cabo hace algunos años) al estudio del comportamiento asintótico de los polinomios de Appell reescalados (familia que incluye a los polinomios de Bernoulli, Euler, Hermite y Laguerre). Dada una sucesión de polinomios p_n, a menudo es interesante localizar sus ceros y, después de reescalar el argumento de una manera apropiada, determinar las curvas límite (atractores) a las que se acercan cuando n tiende a infinito. Además, es importante averiguar el comportamiento asintótico de estos polinomios en este límite (ver Advances in Applied Mathematics 113 (2020) 101962). Estas ideas juegan un papel relevante en el estudio mediante métodos de mecánica estadística de las transiciones de fase en sistemas termodinámicos.

Durante el año hemos continuado con nuestro trabajo sobre la descripción hamiltoniana de los sistemas gravitatorios, en particular hemos puesto a punto un enfoque novedoso (que se basa en el algoritmo de Gotay, Nester, Hinds y otros métodos que hacen uso directo de las ecuaciones de campo) y los aplicamos al estudio de la acción de Holst, a partir de la cual puede obtenerse la formulación de Ashtekar real para la relatividad general. En 2021 aparecerán varios artículos sobre este tema, algunos de ellos completados durante 2020 (ver arXiv: 2011.00661 [gr-qc]). El resultado más importante a este respecto es la identificación de una descripción hamiltoniana muy simple, totalmente invariante de Lorentz, para la relatividad general a partir de la cual es posible obtener la formulación habitual de Ashtekar.

Líneas de Investigación:

• Relatividad General Clásica y Cuántica.
• Cosmología Cuántica de Lazos.
• Teoría Cuántica de Campos en Espaciotiempos Curvos.
• Gravedad no-local.
• Espaciotiempos multiescala.
• Ondas gravitacionales (Consorcio LISA).
• Teorías de campos y geometría.
• Combinatoria y teoría de números.

Labor Investigadora

Durante 2019, el grupo de Gravitación y Cosmología ha progresado en la implementación del enfoque híbrido para la cuantificación de sistemas cosmológicos con perturbaciones primordiales en el marco del formalismo de la gravedad cuántica de lazos. Uno de los pasos principales en este enfoque es la cuantización de las perturbaciones de los campos mediante una representación de Fock. Hemos investigado una posible forma de determinar esta representación de Fock para backgrounds que corresponden a universos planos, homogéneos e isótropos. En más detalle, hemos explorado la posibilidad de seleccionar un estado de vacío natural para las perturbaciones cosmológicas invariantes de gauge, tanto escalares como tensoriales, en el contexto de la cosmología cuántica híbrida mediante la identificación de aquellas variables para la descripción de las perturbaciones que muestran un comportamiento dinámico adaptado de una manera específica a la evolución de la totalidad de la cosmología estudiada. Hemos utilizado una formulación canónica de todo el sistema cosmológico (formado por la geometría de background y las perturbaciones) en el que los grados de libertad perturbativos invariantes de gauge se identifican como variables canónicas. Al introducir en estas perturbaciones transformaciones canónicas lineales dependientes del background que respetan las simetrías espaciales del background y completar esas transformaciones canónicas para todo el sistema, hemos podido caracterizar una colección genérica de variables de creación y destrucción que obedecen la dinámica dictada por una respectiva colección de hamiltonianos. A continuación, hemos impuesto que tales hamiltonianos no posean términos de auto-interacción, de modo que, en una representación de Fock con un orden normal, actúen diagonalmente sobre la base de estados de n partículas. Esto conduce a una ecuación diferencial parcial de primer orden semilineal con respecto al background para los coeficientes que definen las variables de creación y detrucción de los modos de Fourier, así como a una caracterización ultravioleta muy precisa de las mismas. Dicha ecuación de primer orden contiene, en la parte imaginaria de sus soluciones complejas, la complicada ecuación de campo de segundo orden que típicamente surge para la frecuencia dependiente del tiempo de las perturbaciones en el contexto de la teoría cuántica de campos sobre espacio-tiempos curvos. Hemos comprobado que el conocimiento asintótico adquirido permite seleccionar el vacío estándar en los espacio-tiempos de Minkowski y de Sitter. Además, hemos discutido la relación de nuestro vacío y los llamados vacíos adiabáticos, y comprobado que nuestra caracterización asintótica de variables con un hamiltoniano diagonal muestra las propiedades que serían deseables para un estado adiabático de orden infinito.

Nuestro procedimiento para seleccionar un vacío cuántico único para las perturbaciones en el contexto de la cosmología cuántica de lazos híbrida también se ha extendido al caso de un campo de Dirac, mínimamente acoplado al fondo cosmológico y tratado como una perturbación. De esta manera, hemos demostrado que es posible obtener una ecuación de Schrödinger para los grados de libertad fermiónicos que conducen a relaciones de Heisenberg y transformaciones de evolución de Bogoliubov asintóticamente diagonales, sin divergencias en el Hamiltoniano asociado, definido con orden normal. Para este campo de Dirac, también hemos explorado en detalle la relación entre la representación de Fock seleccionada por un criterio de evolución dinámica unitaria (introducida en el pasado por nosotros y más débil que el requisito de diagonalización asintótica) y aquellas construidas con el esquema adiabático familiar de la teoría cuántica de campos en espacio-tiempos curvos. Hemos encontrado que todos los estados adiabáticos pertenecen a la familia de representaciones de Fock que permiten una evolución cuántica implementable de forma unitaria (aunque lo contrario no es generalmente cierto). En particular, esta unitaridad de la dinámica asegura que los vacíos definidos con condiciones iniciales adiabáticas en diferentes momentos son unitariamente equivalentes. También hemos visto que, para todos los órdenes adiabáticos distintos de cero, estas condiciones iniciales permiten la definición de operadores de creación y destrucción para el campo de Dirac que conducen a una backreaction inversa finita en la ligadura hamiltoniana cuántica y a un operador hamiltoniano fermiónico que está bien definido en el span de los estados de n-partículas/antipartículas, en el contexto de la cosmología cuántica híbrida.

Finalmente, también hemos investigado nuevas propuestas para la regularización de la ligadura hamiltoniana en la cosmología cuántica de lazos, centrando nuestra atención en una regularización sugerida por Dapor y Liegener. Hemos cuantizado el Hamiltoniano resultante siguiendo una prescripción de cosmología propuesta por nuestro grupo en años anteriores. Para este efecto, primero hemos regularizado las partes euclídea y lorentziana de la ligadura hamiltoniana por separado en el caso de una cosmología de Bianchi de tipo I. Esto nos ha permitido identificar una simetrización natural del hamiltoniano que resulta evidente en escenarios anisotrópos. Preservando esta simetrización en regímenes isótropos, hemos determinado la ligadura hamiltoniana correspondiente a una cosmología homogénea e isótropa, que luego hemos procedido a cuantizar. Hemos calculado la acción de este operador hamiltoniano en la base propia del volumen y hemos demostrado que toma la forma de una ecuación en diferencias de cuarto orden, en contraste con lo que ocurre en cosmología cuántica de lazos estándar, donde se sabe que es de segundo orden. Hemos investigado los sectores de superselección de nuestro operador de ligadura, demostrando que son semirredes con soporte solo en el semieje positivo o negativo, dependiendo de la orientación de la tríada. Sorprendentemente, el desacoplo entre semiejes nos permite escribir una expresión cerrada para las funciones propias generalizadas de la parte geométrica de la ligadura. Esta expresión está totalmente determinada por los valores en los dos puntos de la semirred que están más cerca del origen, es decir, las dos contribuciones con el volumen propio más pequeño. Esto difiere claramente de la situación encontrada para el Hamiltoniano estándar de cosmología cuántica de lazos, donde solo el valor más pequeño es libre.

También hemos demostrado que los detectores uniformemente acelerados pueden presentar características térmicas incluso cuando la condición KMS no se satisface. Estas características incluyen balance detallado y una respuesta planckiana. Extraemos las condiciones necesarias y suficientes para que la respuesta sea térmica en el límite adiabático. Proporcionamos un modelo sólido para analizar sin ambigüedades la robustez del efecto Unruh frente a deformaciones de las teorías cuánticas de campos (quizá con violaciones Lorentz). También hemos estudiado la magnitud de los efectos de gravedad semiclásica cerca de la formación de un horizonte de agujero negro. Hemos calculado el tensor de energíamomento renormalizado y la función de temperatura efectiva. En particular, hemos analizado las consecuencias de una oscilación justo sobre el radio de Schwarzschild, un acercamiento monótono a este en tiempo infinito y un cruce a diferentes velocidades. Para colapsos con evolución relativista general, recuperamos el paradigma estándar con diminutos efectos semiclásicos. En regímenes más generales, obtenemos una variedad de efectos: desde la emisión de radiación similar a la de Hawking sin formación de horizontes hasta grandes valores del tensor de energía-momento renormalizado vinculados al vacío de Boulware.

El grupo ha continuado trabajando sobre los aspectos geométricos de la formulación hamiltoniana de sistemas lagrangianos singulares, en particular aquellos relevantes para el estudio clásico de teorías de tipo gravitatorio y su cuantización. En este momento se está prestando mucha atención al estudio de teorías de campos definidas en regiones espaciales con fronteras. Estos modelos son relevantes en todas las ramas de la física, ya que las fronteras son muy importantes en los sistemas físicos reales. En el contexto de la física gravitacional, por ejemplo, aparecen como horizontes en los agujeros negros y juegan un papel muy importante en los modelos holográficos. También son de suma importancia para la física teórica de la materia condensada. La presencia de fronteras hace que sea difícil obtener las formulaciones hamiltonianas correctas con los métodos estándar (bastante formales) utilizados hasta ahora. Uno de los problemas es la dificultad para trabajar con la estructura simpléctica canónica cuando hay fronteras. La forma obvia de salir de este tipo de situación es utilizar métodos geométricos. Durante los últmos años, los miembros del grupo (Barbero, Margalef y Villaseñor) han adaptado el llamado método GNH para el tratamiento hamiltoniano de las teorías de campos con fronteras.

Durante el año 2019, hemos desarrollado, en colaboración con el Dr. Bogar Díaz Jiménez, una implementación geométrica práctica del algoritmo de Dirac de forma que se evitan de manera efectiva los problemas que generalmente surgen al considerar fronteras. Una de las razones por las que nuestro método funciona tan bien es el hecho de que la estabilidad dinámica de las ligaduras hamioltonianas se interpreta geométricamente como una condición de tangencia de los campos vectoriales hamiltonianos en el espacio de fases. Esto nos permite evitar el uso explícito de los corchetes de Poisson más allá de la determinación inicial de esto campos vectoriales hamiltonianos, eliminando así algunas de las dificultades habituales. Como aplicación inicial del nuevo método, hemos estudiado una rica familia de acciones gravitatorias en una variedad de cuatro dimensiones con frontera y hemos mostrado cómo la dinámica en el bulk (que admite interpretación dinámica simple ya que viene dada por las ecuaciones de campo del modelo de Husain-Kuchar) interactúa con la dinámica en la frontera (dada por la extensión propuesta por Baekler y Mielke de la relatividad general en 2 + 1 dimensiones). En este momento estamos completando el estudio de varias teorías de campos interesantes con nuestros nuevos métodos hamiltonianos, entre ellas la versión parametrizada de una teoría de Maxwell-Chern-Simons para k-formas en espacio-tiempos de dimensión impar con fronteras y la versión parametrizada de la gravedad unimodular en la formulación de Ashtekar.

Durante el último año, los miembros del grupo (Barbero y Villaseñor), en colaboración con el Dr. Jesús Salas (UC3m) y el Dr. Juan Margalef-Bentabol (Penn State University) han continuado su trabajo en combinatoria y temas relacionados, en particular el uso de métodos asintóticos para el estudio y caracterización de las propiedades de los conjuntos de ceros de familias de polinomios (en particular, los polinomios de Appell). Este trabajo es un subproducto interesante del realizado en el pasado sobre el estudio de la entropía de los agujeros negros y el operador del área en Gravedad Cuántica de Lazos.

En el contexto de la gravedad no-local, hemos aclarado por primera vez la estructura del espectro no-perturbativo de la teoría, demostrando que el gravitón es el único grado de libertad físico que propaga en espaciotiempos planos o con escalar de Ricci nulo (también se demostró la estabilidad de estos espaciotiempos como soluciones exactas). Otros grados de libertad, nuevos respecto a los de la relatividad general, pueden propagar en ciertos fondos curvos. Ninguno de los modos fantasmas de las teorías gravitatorias locales de orden superior está presente en el espectro físico, quedando así garantizada la unitariedad de la teoría no-local a nivel árbol.

Este año marca la entrada del grupo en el Consorcio LISA, específicamente en los Cosmology Working Group y el Fundamental Physics Working Group. La principal actividad científica relacionada con este experimento espacial, cuyo inicio está previsto para 2034, fue el estudio de la distancia de luminosidad de las ondas gravitacionales de origen astrofísico en teorías de gravedad modificada o de gravedad cuántica. Es la primera vez que se aborda el problema de cómo modelos tipo DHOST o correcciones de gravedad cuántica pueden distorsionar la distancia de luminosidad y con qué tamaño del efecto. Con los miembros del LISA Cosmology Working Group, hemos estudiado dichos efectos tanto a nivel teórico como en simulaciones numéricas utilizando catálogos simulados de sirenas estándar detectables por LISA. El resultado, publicado en un artículo oficial de la Colaboración, es que sí existen algunos modelos cuyas correcciones pueden llegar al umbral de sensitividad del instrumento. En estas teorías más allá de la gravedad de Einstein, las ondas gravitacionales propagan de una forma característica discriminable respecto a la física ordinaria. En otros dos artículos no pertenencientes a LISA, pero en colaboración con miembros de LISA y LIGO, hemos explorado estos detalles en el ámbito de una amplia clase de teorías de gravedad cuántica.

Líneas de Investigación:

• Relatividad General Clásica y Cuántica.
• Cosmología Cuántica de Lazos.
• Teoría Cuántica de Campos en Espaciotiempos Curvos.
• Gravedad no-local.
• Espaciotiempos multiescala.
• Ondas gravitacionales (Consorcio LISA).
• Teorías de campos y geometría.

Labor Investigadora

En los últimos años, la Cosmología Cuántica de Lazos (CCL) se ha aplicado para extender el análisis de las perturbaciones primordiales a la era de Planck y discutir los posibles efectos de la geometría cuántica en el fondo cósmico de microondas. Dos enfoques para CCL con un comportamiento ultravioleta admisible que conducen a predicciones que son compatibles con las observaciones son el formalismo híbrido, propuesto por nuestro Grupo en el IEM, y el de métrica vestida, propuesto por Ashtekar y sus colaboradores. A pesar de sus similitudes y relaciones, en 2018 hemos demostrado que las ecuaciones efectivas que estos dos formalismos proporcionan para la evolución de las perturbaciones primordiales tensoriales y escalares resultan ser algo diferentes. Cuando se ignora la backreaction, la discrepancia aparece solo en el término de masa dependiente del tiempo de las ecuaciones de campo correspondientes. Hemos explicado cómo surge esta diferencia debido a los distintos procedimientos de cuantización seguidos. Además, dado el rol privilegiado que desempeña el rebote (big bounce) en CCL, por ejemplo, como un instante de tiempo natural para establecer las condiciones iniciales para las perturbaciones, hemos analizado la positividad de la masa dependiente del tiempo cuando se produce este rebote. Hemos comprobado que la masa de las perturbaciones tensoriales es positiva en el formalismo híbrido cuando la contribución cinética a la densidad de energía del inflatónJu domina sobre su potencial, así como para un sector de soluciones de fondo considerablemente grande alrededor de esa situación, mientras que dicha masa resulta ser siempre no positiva en el formalismo de métrica vestida. Resultados similares también son válidos para las perturbaciones escalares.

También hemos analizado el paso a un límite continuo de los modos de Fourier de las perturbaciones primordiales en espaciotiempos cosmológicos en CCL. Hemos demostrado que este límite puede alcanzarse incluso si uno comienza considerando una celda fiducial finita como sección espacial. Hemos centrado nuestra atención en los regímenes en los que la geometría de fondo sigue la denominada dinámica efectiva de CCL, aunque nuestros argumentos pueden extenderse más allá de este régimen y a otros formalismos en Cosmología. Si bien el sistema perturbado puede describirse de manera invariable frente a cambios del volumen fiducial utilizando variables adecuadas, hemos demostrado que el límite continuo deseado puede establecerse, más bien, por medio de transformaciones de escalado del volumen físico cuando este volumen crece sin límites. Estas transformaciones conducen a un modelo con un continuo de modos e independiente de cualquier escala de referencia para el volumen físico.

Además, hemos investigado el papel desempeñado por el vacío de las fluctuaciones primordiales en CCL híbrida. Hemos considerado escenarios en los que el potencial del inflatón es un término de masa y la geometría cuántica no perturbada se rige por la dinámica efectiva de CCL. En esta situación, las soluciones fenomenológicamente interesantes tienen un régimen preinflacionario en el que la energía cinética del inflatón domina sobre el potencial. Para este tipo de soluciones, hemos demostrado que los espectros de potencia primordiales dependen en gran medida de la elección del vacío. Hemos estudiado en detalle el caso de estados adiabáticos de bajo orden, y el vacío no oscilante introducido en nuestro Grupo, todos ellos impuestos en el rebote. Los espectros adiabáticos, generalmente, resultan estar suprimidos a escalas grandes, y muestran oscilaciones rápidas con un aumento de potencia en escalas intermedias. En el vacío no oscilante, por otra parte, hay una supresión de potencia para escalas grandes, pero las oscilaciones rápidas están ausentes. Hemos argumentado que las oscilaciones se deben a la imposición de condiciones adiabáticas iniciales en la región de dominio cinético, y que también estarían presentes en Relatividad General. Además, hemos discutido la sensibilidad de nuestros resultados a cambios del tiempo inicial y de otros datos del modelo.

Finalmente, hemos discutido la libertad disponible en CCL híbrida para definir variables canónicas para el contenido de materia, y hemos investigado si esto se puede usar para derivar una teoría de campo cuántica con buenas propiedades para el sector material. Más específicamente, hemos centrado nuestro estudio en el caso de perturbaciones fermiónicas de tipo Dirac en un espacio-tiempo cosmológico. En particular, hemos analizado la posibilidad de obtener una reacción fermiónica finita, así como un hamiltoniano que esté definido densamente en el espacio de Fock y que, a la vez, dicte la dinámica de Schrödinger asociada con la evolución de las variables de creación y destrucción elegidas para las perturbaciones fermiónicas.

La gravedad cuántica no-local es una teoría de campos renormalizable y unitaria de la gravedad que contiene operadores con infinitas derivadas. Este año ha sido marcado por tres hitos fundamentales, desarrollados por nuestro grupo (uno de los más activo a nivel internacional sobre esta teoría). En primer lugar, hemos resuelto el problema de Cauchy y demostrado que la dinámica requiere solo un número finito de condiciones iniciales en la métrica, así extendiendo por primera vez resultados análogos de 2007 para un campo escalar. En paralelo, hemos podido contar de forma rigurosa el número de grados de libertad no-perturbativos de la teoría, también finitos. Estos resultados permiten dar un sentido físico a las soluciones dinámicas clásicas. En tercer lugar, hemos demostrado que todas las métricas con tensor de Ricci nulo son soluciones estables de la teoría. Eso implica que también Schwarzschild es solución y la teoría admite agujeros negros singulares, contrariamente a la idea general de que la no-localidad es suficiente para resolver las singularidades de la relatividad general. Actualmente se está estudiando si estas soluciones son físicas o no.

Respecto a los espaciotiempos multiescala, generados dentro de gravedades cuánticas, utilizamos nuestros avances notables de 2017 para empezar la fase más fundamental de la teoría, es decir, la construcción de la llamada dinámica con derivadas fraccionarias. Un estudio preliminar sobre las propiedades matemáticas de estos operadores ha evidenciado la necesidad de replantear algunas de las ideas iniciales, que verán su maduración en 2019. En paralelo, hemos puesto las cotas observacionales más fuertes hasta el momento (procedentes de tests de precisión del Modelo Estándar de interacciones electrodébiles) para los modelos ya desarrollados.

Por último, en 2018 uno de los miembros del grupo ha entrado en el Consorcio LISA, en los Grupos de Trabajo de Cosmología y Física Fundamental. LISA es un interferómetro espacial de la ESA/NASA operativo a partir de 2034 que detectará ondas gravitacionales de objetos astrofísicos a redshift grande, como por ejemplo agujeros negros súper masivos y sistemas binarios rápidos. A pesar del hecho de que estamos todavía lejos para aprovechar de los datos de LISA, hay una intensa actividad para completar la llamada Fase A del experimento, donde se finalizarán los detalles del diseño instrumental y la ciencia que podremos hacer con ello. En los Grupos de Trabajos teóricos, estamos explorando la posibilidad de poner cotas observacionales sobre modelos de gravedad modificada y gravedad cuántica. Los dos proyectos en curso terminarán en los primeros meses de 2019 y no hay publicaciones para 2018. Sin embargo, hay que resaltar el crecimiento de las relaciones a nivel nacional e internacional de nuestro grupo con otros trabajando en el Consorcio o, incluso, en los proyectos multiautor arriba mencionados. Dicha actividad ha sido acompañada por un aumento de experiencia científica en este campo, lo que puede jugar un papel importante en la investigación futura en el IEM.

Como aplicación de los métodos combinatorios desarrollados por los miembros del grupo para problemas relevantes en gravedad cuántica, hemos utilizado una serie de ideas introducidas en el estudio de sistemas cuánticos lineales compuestos para la resolución de algunos problemas en Gravedad Cuántica de Lazos (LQG). En particular, hemos estudiado el comportamiento del espectro de operadores geométricos, como el de área, relevantes en el estudio de los agujeros negros en LQG. Mediante una generalización de las funciones generatrices habituales obtenida utilizando transformadas de Laplace y Mellin, hemos podido determinar el comportamiento asintótico de la densidad de los autovalores del operador de área en el límite de áreas grandes y también una representación muy precisa para esta cantidad en la zona del espectro correspondiente a áreas pequeñas. Por el camino, hemos obtenido identidades, hasta ahora desconocidas, sobre los números de Bernoulli (un interesante resultado colateral de nuestro uso de métodos combinatorios y de teoría de números).

Otro desarrollo interesante, esta vez dentro del ámbito de la teoría cuántica de campos en espaciotiempos curvos, ha sido la introducción de un método eficiente para extender las técnicas de regularización y renormalización adiabáticas al tratamiento de los campos de Dirac en cosmología cuántica. La idea crucial a este respecto fue encontrar una manera de escribir la ecuación de evolución para las funciones del tiempo que describen los modos de Fourier del campo de Dirac como una ecuación de Schrödinger dependiente del tiempo para un Hamiltoniano matricial de dimensión dos por dos. A partir de esto, logramos encontrar un esquema de resolución perturbativo compatible con la aproximación adiabática. La solución fue construida mediante un procedimiento iterativo que nos permitió escribirla como un producto de operadores unitarios. Las propiedades de simetría de la solución así obtenida han facilitado la comprensión de algunas características de los resultados conocidos sobre este problema. Específicamente, hemos podido utilizar este nuevo enfoque para recuperar los resultados conocidos sobre anomalías conformes y de traza en varios modelos de interés cosmológico (con acoplos de tipo Yukawa y campos electromagnéticos).

Hemos propuesto y estudiado en detalle una propuesta de un método para medir directamente la función de dos puntos en campos cuánticos. Con el objetivo de adquirir una comprensión más profunda de los campos gravitatorios intensos, hemos llevado a cabo un análisis de la inestabilidad debida a la presencia de ergorregiones en sistemas cuánticos rotantes, llegando a la conclusión de que existen regiones de metaestabilidad en el espacio de parámetros. También hemos diseñado un método para tener en cuenta las no localidades (posiblemente originadas por efectos cuánticos en teorías efectivas) en la teoría de campos mediante la introducción de un grado de libertad adicional relacionado con la escala del sistema. Nos hemos enfrentado al problema de la constante cosmológica desde el punto de vista de la teoría de campos relativistas aplicada a la gravedad argumentando que, quizá, no es un problema en absoluto.

Líneas de Investigación:

• Gravedad y Cosmología Cuántica de Lazos.
• Relatividad General Clásica y Cuántica.
• Teorías de gravedad cuántica y geometría multi-fractal.
• Gravedad y teorías de campos no-locales.
• Agujeros negros.
• Teorías de campos y geometría.

Labor Investigadora

Durante 2017, el Grupo de Gravitación y Cosmología ha realizado progresos sustanciales en la investigación de criterios que seleccionan una única representación de Fock de campos cuánticos en espaciotiempos curvos. Esta línea de investigación es de máximo interés en cosmología, ya que permite extraer resultados robustos, eliminando ambigüedades en las predicciones cuánticas que de otra manera plagarían la teoría. Estos resultados de unicidad también son importantes en la medida en que proporcionan una forma única de separar la dinámica cuántica de los campos de la del espaciotiempo de fondo, algo que es necesario si también se quiere proceder a una descripción cuántica de la geometría. Además, los resultados tienen aplicaciones en otras áreas de la física, como la información cuántica o la materia condensada, ya que permite determinar una familia única de vacíos en situaciones donde el fondo no es estacionario, y dar una descripción muy adecuada de la dinámica si uno quiere discutir temas como la conservación de la información. Nuestro Grupo ha logrado ampliar sus resultados anteriores sobre los criterios que seleccionan una familia única de cuantizaciones de Fock equivalentes para campos escalares en fondos homogéneos e isótropos, extendiéndolos al caso de algunos espaciotiempos anisótropos. Además, los resultados se han generalizado también a campos de Dirac en escenarios cosmológicos. Utilizando esta generalización y combinando la cuantización de Fock de los campos fermiónicos con una cuantización de lazos de la geometría, se ha llevado a cabo un análisis completo de las perturbaciones cosmológicas en presencia de un campo de Dirac (tratado también como una perturbación). Se ha demostrado que los fermiones no afectan significativamente las perturbaciones cosmológicas en las eras pre-inflacionarias e inflacionarias, siempre que el vacío se elija en la familia escogida por nuestros criterios. Además, entre los vacíos de esta familia, hay suficiente libertad para seleccionar un vacío adecuado de modo que la contribución de los fermiones al hamiltoniano se haga finita y no necesite regularización.

En añadidura a estos estudios, el Grupo ha investigado en gran detalle, tanto analítica como numéricamente, las consecuencias de una cuantización híbrida en el marco de la cosmología cuántica de lazos para las perturbaciones primordiales, obteniendo predicciones para el fondo cósmico de microondas y comparándolas con los datos recopilados por la misión Planck. Con este objetivo, se han completado análisis previos sobre las perturbaciones escalares y se han incorporado modos tensoriales. Se ha calculado el espectro de potencia de estas perturbaciones para una variedad de estados de vacío, analizando la relación tensor-escalar y la relación de consistencia entre esta cantidad y el índice espectral tensorial. El Grupo ha calculado las funciones de correlación temperatura-temperatura, eléctrica-eléctrica, temperaturaeléctrica y magnética-magnética. Se han discutido los efectos de la geometría cuántica en estas funciones de correlación y se han confrontado los resultados numéricos con las observaciones.

Durante los últimos años se han desarrollado modelos teóricos en los que efectos cuánticos macroscópicos en agujeros negros pueden dar lugar a modificaciones de las señales de ondas gravitatorias caracterizadas por la existencia de repeticiones amortiguadas de la señal primaria. Por ejemplo, la cuantización del campo gravitatorio puede permitir la existencia de un canal de decaimiento de agujeros negros en agujeros blancos con simetría bajo inversión temporal. Se ha llevado a cabo la integración funcional sobre un conjunto de geometrías con simetría esférica utilizando una sola variable que interpola entre las geometrías de agujero negro y agujero blanco en una región espaciotemporal acotada. Se ha obtenido una distribución de probabilidad finita con un decaimiento exponencial en la anchura de dicha región con una vida media inversamente proporcional a la masa de Schwarzschild. Las propuestas que dan lugar a la existencia de ecos en la señal tardía de ondas gravitatorias producidas en la coalescencia de agujeros negros comparten la característica de que los agujeros negros deben ser reemplazados por configuraciones sin horizontes con una superficie física reflectante en las frecuencias relevantes. Por otro lado, las propuestas que restringen los efectos cuánticos en la geometría externa a los perturbativos, como los obtenidos a partir de la complementariedad, no presentan ecos.

También se ha revisitado la motivación y la construcción de una teoría unificada de la electrodinámica y la gravedad, siguiendo las ideas de Weyl. Se ha visto que las ecuaciones del campo gravitatorio son equivalentes a las de Einstein (sin traza), asegurando así la compatibilidad con los tests de la relatividad general. Por tanto, la constante cosmológica efectiva resulta ser radiativamente estable debido a la invariancia Weyl. Esto también conlleva la existencia de una energía por debajo de la que la no integrabilidad de las distancias espaciotemporales y la masa efectiva del campo electromagnético aparecen simultáneamente. También se ha visto que las críticas previas en contra de las ideas de Weyl pierden su poder en esta versión.

El año 2017 ha marcado un importante avance en el estudio de las llamadas teorías multi-fraccionarias, un enfoque de gravedad cuántica que ha sido desarrollado en nuestro departamento a partir de 2012. En estas teorías de gravedad y de campos, la estructura del espaciotiempo es la típica de los multi-fractales. Hemos puesto cotas observacionales muy fuertes procedentes tanto de las recientes observaciones de ondas gravitatorias por parte de LIGO como de los eventos de rayos cósmicos de energía ultra-elevada. Además, hemos cuantificado y especificado la relación entre estas teorías y los enfoques de espaciotiempos no-conmutativos; dicha relación fue conjeturada hace bastante tiempo sin haber nunca sido aclarada de manera satisfactoria, hasta la fecha de hoy. Hemos encontrado que los dos enfoques son independientes, a pesar de muchas similitudes. El hito más importante, sin embargo, ha sido la formulación de un principio geométrico que determina de forma unívoca la medida de la geometría, así consagrando las teorías multi fraccionarias y sus parientes con medidas no-factorizables como los únicos candidatos para describir geometrías espaciotemporales genuinamente multifractales. Todo esto se recoge también en un artículo de revisión que constituye el manifesto más actualizado de este enfoque teórico. Posteriormente, se abordaron otros aspectos de la teoría, incluso el comportamiento de agujeros negros y la posibilidad de huellas observables en la radiación cósmica de fondo, más otro logro fundamental: es decir, el “descubrimiento” teórico de que el flujo dimensional (el cambio de la dimensión del espaciotiempo con la escala de observación) típico de todas las gravedades cuánticas es físicamente equivalente al fenómeno de la borrosidad, donde las incertidumbre en mediciones físicas es debida a fluctuaciones cuánticas de la geometría del espaciotiempo. El establecimiento de esta dualidad conlleva una parsimonia conceptual que tendrá consecuencias no solo en las teorías multi-fraccionarias, sino también en todas las demás gravedades cuánticas.

Utilizando las mismas herramientas de geometría anómala empleadas en las teorías multi-fraccionarias, hemos también demostrado un teorema que relaciona la dimensión espectral del espaciotiempo y la posibilidad de obtener una entropía de entrelazamiento del espaciotiempo finita. Este trabajo recibió una Mención de Honor en los 2017 Awards for Essays on Gravitation de la Gravity Research Foundation.

Por último, respecto al enfoque de la gravedad cuántica no-local (independiente de los ya mencionados) donde la dinámica es caracterizada por operadores con infinitas derivadas, hemos demostrado que las soluciones de Schwarzschild (agujero negro) existen y son estables, al menos en una versión específica de dicha teoría. Esto implica que las teorías no-locales no están exentas de singularidades, contrariamente a lo que se había creído hasta hoy. Por tanto, por sí misma la no - localidad es insuficiente para garantizar la ausencia de infinitos. Queda por demostrar esta conclusión para las versiones súper-renormalizables de la teoría.

Por lo que respecta al trabajo sobre la formulación hamiltoniana de teorías de campos no estándar (modelos que acoplan objetos de diferentes dimensiones y en regiones espaciales acotadas con condiciones de contorno generales) los principales resultados obtenidos se refieren a la implementación unitaria de la dinámica cuántica en modelos de campos escalares en dimensión 1 + 1 sujetos a condiciones de contorno de tipo Dirichlet, Neumann o Robin y la introducción de operadores de traza en el contexto de la cuantización de sistemas unidimensionales acoplados a partículas puntuales.

En lo que se refiere al primer tema, el principal resultado que hemos obtenido es la caracterización de las clases de equivalencia de embeddings espaciales para los que es posible tener evolución unitaria. Hasta la fecha este tipo de análisis había sido realizado solo para el caso del círculo, donde no se necesitan condiciones de contorno. La introducción de fronteras restringe la clase de secciones espaciales en las que es posible tener evolución unitaria, lo que nos obliga, por lo tanto, a obtener una caracterización concreta de los mismos. Nuestros resultados no solo proporcionan una comprensión útil de la cuantización de Fock de estos modelos en foliaciones espaciotemporales generales, sino que también pueden ser útiles para estudiar esquemas más exóticos de cuantización, como los poliméricos.

Los resultados en teorías de campos en las que se acoplan objetos de diferentes dimensiones complementan los obtenidos por el grupo en años anteriores. En particular, hemos hecho una propuesta concreta para introducir espacios de Hilbert auxiliares para los objetos dinámicos situados en los bordes y los operadores necesarios para describir su dinámica (los llamados operadores de traza). Este es un problema interesante porque los espacios de Hilbert de estos modelos compuestos no pueden ser factorizados como productos tensoriales de espacios de Hilbert asociados de forma natural con la parte continua (cuerda) y las partículas puntuales unidas a sus extremos. El conocimiento actual sobre este tipo de sistemas abre la posibilidad de usarlos para modelar fenómenos cuánticos complicados relacionados con el problema de medición y el estudio del límite clásico, que planeamos abordar en el futuro inmediato.

Líneas de Investigación:

• Gravedad y Cosmología Cuántica de Lazos.
• Relatividad General Clásica y Cuántica.
• Cosmología cuántica.
• Agujeros negros.
• Combinatoria.
• Teoría cuántica de campos.
• Teorías de gravedad cuántica y geometría multi-fractal.

Labor Investigadora

Durante el año 2016, el Grupo de Gravitación y Cosmología ha continuado el estudio de las técnicas de cuantización de campos en cosmología y de la aplicación de dichas técnicas a la investigación de perturbaciones cosmológicas y otros escenarios de interés en astrofísica relativista, así como a sistemas análogos en física de materia condensada. Parte de la investigación se ha dedicado a la determinación de criterios capaces de asegurar la unicidad de la cuantización de Fock de campos fermiónicos en espaciotiempos cosmológicos, y por lo tanto lejos de la estacionariedad. Este estudio de los fermiones generaliza trabajos previos del Grupo sobre la cuantización de Fock de campos escalares y perturbaciones tensoriales. De manera similar a la situación que se había encontrado para esos campos escalares y tensoriales, aunque enfrentando ahora una complejidad mucho más rica, estos criterios seleccionan también una dinámica esencialmente única para los campos fermiónicos en este tipo de espaciotiempos curvos, llevando a una separación natural entre el fondo cosmológico y unas variables de campo que evolucionan unitariamente. Para los fermiones, esta separación no es un mero rescalado del campo. Hacemos notar que la unitaridad de la evolución garantiza que la coherencia cuántica de los fermiones se preserva: no ocurre ninguna pérdida de información para partículas fermiónicas adaptadas a esta noción de dinámica, para la que se ha extraído adecuadamente la dependencia en el fondo.

Hemos avanzado aún más en la aplicación de estos criterios de unicidad al considerar la cuantización de Fock de campos escalares en espaciotiempos de tipo Bianchi I. De nuevo, hemos demostrado que estos criterios garantizan la unicidad en la elección de una dinámica que respeta la unitaridad, así como de la representación de Fock para las relaciones de conmutación canónicas asociadas. Esta es la primera vez que nuestros criterios de unicidad se han implementado en espaciotiempos anisótropos. El éxito de nuestra propuesta abre nuevas vías para la cuantización de campos de materia y perturbaciones en escenarios anisótropos en cosmología cuántica.

Además, hemos combinado estos resultados sobre la cuantización de Fock en espaciotiempos curvos con el enfoque híbrido introducido por nuestro Grupo en Cosmología Cuántica de Lazos (Loop Quantum Cosmology en inglés), con el objetivo de analizar las consecuencias de la cuantización simultánea de los campos de materia y de la geometría en la formación y desarrollo de las perturbaciones cosmológicas. Hemos extraído ecuaciones modificadas para las perturbaciones cosmológicas,que retienen estos efectos de gravedad cuántica y que podrían conducir a predicciones falsificables, por ejemplo en el fondo cósmico de microondas. Asimismo, hemos generalizado nuestro estudio a esquemas de cuantización en cosmología distintos de la Gravedad Cuántica de Lazos. De esta manera, hemos construido un marco generalizado para nuestro enfoque híbrido que se ha mostrado consistente y capaz de incorporar todas las modificaciones de geometría cuántica al espectro primordial de las perturbaciones, más allá de las típicas aproximaciones semiclásicas empleadas usualmente en cosmología cuántica.

Otro tema que hemos investigado es si el efecto ultravioleta dominante en el colapso gravitatorio de estrellas masivas puede ser una transición de agujero negro a agujero blanco. Estudiando el cruce entre capas esféricas nulas en geometrías que describen esta transición, hemos obtenido las condiciones para que aparezca la llamada inestabilidad de Eardly. Las transiciones con tiempos característicos largos son patológicamente inestables, mientras que las que tienen tiempos característicos cortos son robustas frente a perturbaciones, de manera que los procesos correspondientes podrían tener lugar en escenarios astrofísicos. También hemos construido una descripción tensorial de la percepción de partículas en un agujero negro y hemos establecido una clara separación entre la parte radiativa (de Hawking) y la contribución del efecto Unruh a las medidas de un detector en un agujero negro; a la vista de esto hemos argumentado que cruzar lentamente un horizonte de agujero negro podría no ser posible. Desde otro punto de vista, hemos estudiado el proceso de termalización para detectores de partículas en el efecto Unruh y también la posibilidad de transmitir información en intervalos temporal es con campos sin masa en escenarios cosmológicos. Finalmente hemos analizado cómo las simetrías físicas pueden dar lugar a simetrías gauge emergentes en el caso de un campo vectorial.

En paralelo, las llamadas teorías multi-fraccionarias (teorías de gravedad cuántica donde la estructura del espaciotiempo es la típica de los multi-fractales) han experimentado un desarrollo notable gracias a nuestros esfuerzos. Por un lado, se ha formulado por primera vez una definición de geometría fractal lorentziana y una clasificación de las teorías de gravedad cuántica según el tipo de flujo dimensional que les caracteriza. Hemos construido rigurosamente el Modelo Estándar de interacciones electrodébiles y fuertes en dos teorías multi-fraccionarias (con derivadas con peso y con derivadas de tipo q), a partir de las simetrías de la acción. Se completó así la formulación teórica y conceptual de estas teorías. Por otro lado, hemos logrado obtener una impresionante cantidad de cotas observacionales directas sobre las escalas fundamentales de las geometrías multi-escala, procedentes de la electrodinámica cuántica (variación de la constante de estructura fina y efecto de Lamb shift), de las interacciones débiles (vida media del muón), de observaciones astrofísicas (ondas gravitatorias y GRBs) y de la Radiación Cósmica de Microondas (CMB en inglés). Hemos comparado las teorías multi-fraccionarias con las de gravedad cuántica tradicionales y demostrado como las ondas gravitatorias observadas por LIGO pueden restringir eficazmente, por sí solas, el espacio de los parámetros de dichas teorías, mientras que las mismas observaciones pueden decir muy poco respecto a la escala de energía de gravedades cuánticas. Con la obtención de cotas fuertes sobre las escalas de la medida geométrica, se completa también la fenomenología de dos de las tres teorías multi-fraccionarias.

El descubrimiento de ondas gravitatorias de origen astrofísico por parte de LIGO ha permitido reevaluar la observabilidad de efectos de gravedad cuántica. Dichos efectos se codifican en relaciones de dispersión modificadas que afectan a la propagación de las ondas de geometría en el espaciotiempo. Lamentablemente, las observacio nes de LIGO no ponen cotas fuertes sobre la escala de energía a partir de la cual deberíamos empezar a notar efectos de gravedad cuántica. Nuestro Grupo ha obtenido este resultado tanto para un modelo no-local debido a Padmanabhan como en casos fenomenológicos más generales. Además, nuestras cotas permitieron la primera comparación, a nivel de la fenomenología, entre teorías de gravedad cuántica y teorías multi-fraccionarias.

Por último, hemos concluido el estudio riguroso del flujo dimensional, el cambio de la dimensión efectiva del espaciotiempo (desde la dimensión topológica 4 a grandes escalas hasta un valor menor a escalas de Planck) observado en virtualmente todas las gravedades cuánticas, tanto en enfoques continuos como discretos. Hemos también definido la dimensión espectral en el marco de teorías de campos, solucionando así algunos problemas conceptuales que surgen en la interpretación tradicional de la dimensión espectral en términos de un proceso de difusión. Nuestros trabajos consolidan el aparato teórico utilizado en los estudios del flujo dimensional en la literatura de gravedad cuántica.

En el contexto del estudio riguroso de la formulación hamiltoniana para teorías de campos, hemos avanzado en dos direcciones diferentes. Por un lado, hemos prestado atención a la interacción entre las simetrías de gauge internas y los difeomorfismos en modelos parametrizados, en particular el electromagnetismo. Aunque el electromagnetismo parametrizado ha sido considerado en el pasado por varios autores, faltaba una comprensión satisfactoria de sus rasgos más sobresalientes, en particular sus simetrías. Es posible resolver este problema de forma satisfactoria utilizando los métodos Hamiltonianos geométricos desarrollados por Gotay, Nester y Hinds a finales de la década de los setenta. En este ejemplo particular hemos encontrado una interacción muy interesante entre la invariancia de gauge y la evolución temporal. Específicamente, hemos demostrado que sólo puede haber dinámica no trivial en el sector de la hipersuperficie de las ligaduras en el que se cumple la ley de Gauss. Fuera de este sector la evolución temporal se congela y el sistema se comporta de manera trivial. Este tipo de comportamiento también puede ser entendido, con algunas dificultades técnicas, como procedente de una bifurcación del algoritmo de ligaduras de Dirac (se da una situación similar en el estudio de modelos de Chern-Simons de dimensión superior). De hecho, los métodos geométricos que utilizamos resultan ser eficaces y de uso sencillo; ciertamente mejores que los enfoques estándar.

Un segundo sistema que hemos analizado en detalle es el campo escalar parametrizado definido en regiones espaciales acotadas. La principal cuestión de interés en este contexto es la incorporación de diferentes tipos de condiciones de contorno. De hecho, una clase importante de ellas (las de tipo Robin) han presentado grandes dificultades que han impedido su comprensión satisfactoria hasta la fecha. En este ejemplo, la cuestión técnica principal está relacionada con el hecho de que los tratamientos estándar (es decir, no geométricos) no son adecuados para tratar con variedades de diferente dimensión (en este caso el volumen y la frontera del espaciotiempo). El uso de métodos geométricos abstractos, con su independencia explícita en las coordenadas, nos permitió eludir los problemas técnicos asociados con la presencia de fronteras. La formulación final que encontramos para el modelo proporciona una extensión consistente de los resultados conocidos para el sistema no parametrizado sujeto a diferentes familias de condiciones de contorno (Dirichlet, Neumann y Robin). Como en el ejemplo del campo electromagnético hay una interacción entre ciertas ligaduras --relevantes sólo en las fronteras-- y la evolución temporal.

Líneas de Investigación:

• Gravedad y Cosmología Cuántica de Lazos.
• Relatividad General Clásica y Cuántica.
• Cosmología cuántica.
• Agujeros negros.
• Combinatoria.
• Teoría cuántica de campos.
• Modelos de gravedad cuántica y geometría multi-fractal.
• Física Matemática.

Labor Investigadora

Cosmología cuántica, agujeros negros y fractales.

Hemos continuado el desarrollo de la línea de investigación del departamento referente a cuantización de sistemas cosmológicos con inhomogeneidades. En concreto, hemos analizado la aplicación al estudio de perturbaciones cosmológicas del formalismo de cuantización híbrida propuesto por nosotros. Este formalismo establece una jerarquía en los fenómenos de geometría cuántica, permitiendo la combinación de técnicas de cosmología cuántica con métodos más convencionales de teoría de campos en espaciotiempos curvos. Hemos profundizado en la discusión de cuáles son las consecuencias de la cuantización híbrida en escenarios inflacionarios. Nuestro esquema de cuantización extiende la dinámica cosmológica a una época preinflacionaria en la que uno esperaría que los efectos de gravedad cuántica fueran importantes. Esto permite comparar predicciones teóricas de modelos cuánticos con los datos observaciones extraídos del fondo cósmico de microondas. Cabe destacar que nuestro estudio de un universo homogéneo e isótropo con campo escalar en presencia de perturbaciones se basa en una formulación que está especialmente diseñada para preservar la covariancia de la Relatividad General, pues parametrizamos las perturbaciones en términos de cantidades invariantes gauge, y no hacemos ninguna fijación de gauge a nivel clásico. También hemos proseguido con nuestras investigaciones sobre la cuantización híbrida del modelo de Gowdy, que es inhomogéneo, pero con simetrías en ciertas direcciones, de manera que los grados de libertad local se propagan en un fondo anisótropo. Hemos generalizado la construcción de soluciones aproximadas a la ligadura hamiltoniana, con un contenido material que consiste en un campo escalar. Las soluciones encontradas tienen un comportamiento muy interesante, ya que representan estados que, siendo de forma inherente inhomogéneos, resultan ser soluciones aproximadas de un modelo cosmológico homogéneo e isótropo, con materia dada por cualquier fluido perfecto (por ejemplo de tipo constante cosmológica), y con posibles modificaciones a la geometría, similares a las estudiadas en teorías modificadas de gravedad, como f(R).

Asimismo, con el objetivo de extender a campos fermiónicos los resultados previos de nuestro grupo sobre la unicidad en la cuantización de Fock de campos que se propagan en espaciotiempos curvos, hemos investigado un campo de Dirac en un fondo cosmológico homogéneo e isótropo, con secciones espaciales cuya topología es la de la tres-esfera. Hemos construido una clase de equivalencia de representaciones de Fock que está seleccionada por los criterios de poseer un vacío que es invariante bajo la acción del grupo de isometrías del fondo cosmológico, y por admitir una implementación unitaria de la dinámica cuántica. 

Existen varias propuestas para regularizar la singularidad clásica de los agujeros negros de forma que su formación y evaporación no dé lugar a problemas de pérdida de información. Una característica común de todas estas propuestas es que estos agujeros regulares presenten horizontes aparentes longevos. Hemos analizado un esquema de regularización de la singularidad clásica que da lugar a un escenario completamente diferente. En nuestro esquema, el colapso de un objeto estelar da lugar a un rebote genuinamente simétrico en el tiempo, lo que en términos geométricos supone la conexión de una geometría de agujero negro con otra de agujero blanco. La duración del rebote visto desde observadores externos es muy corta. Este escenario ha dado lugar a la búsqueda de nuevas formas de equilibrio estelar.

También hemos analizado las implicaciones de la violación del principio de Huygens fuerte en la transmisión de información desde el universo primitivo hasta hoy mediante campos sin masa. Hemos demostrado que hay mucha información que nos llega a través de canales de género tiempo, y no mediados mediante fotones reales.

Las partículas que se mueven en el exterior de una estrella experimentarán en general fricción cuántica causada por la reacción de la radiación Unruh. Existen sin embargo trayectorias que no presentan este. En estas trayectorias, los observadores perciben solo la emisión estelar, sin contribuciones adicionales provenientes del efecto Unruh. Resultan tener la propiedad de que las variaciones del efecto Doppler y de los desplazamientos gravitacionales se compensan. No son geodésicas y su aceleración propia obedece una ley de cuadrado inverso, lo que significa que podría estar generada por radiación estelar saliente. En el caso de un agujero negro que emite radiación de Hawking, esto puede dar lugar a un escenario de flotación.

También hemos analizado el problema de la constante cosmológica, que puede entenderse como un fracaso del principio de desacoplo que subyace en las teorías efectivas de campos, de manera que algunas magnitudes en la teoría de baja energía son extremadamente sensibles a las propiedades de alta energía. Siguiendo esta intuición, hemos considerado una modificación mínima de la estructura de la relatividad general que, como teoría efectiva, permite trabajar de forma consistente a bajas energías, es decir, por debajo de la escala de gravedad cuántica. Esta descripción efectiva preserva la fenomenología clásica de la relatividad general y el espectro de partículas del modelo estándar. El precio que debe pagarse es cambiar nuestra visión conceptual y matemática del espaciotiempo.

Una línea independiente de investigación ha sido el desarrollo teórico y experimental de las teorías de espaciotiempos multi-escala, donde la geometría cambia con la escala de manera similar a las de multi-fractales. Hemos estudiado por primera vez el Modelo Estándar de partículas elementales tanto en el caso clásico como en sus aspectos cuánticos. Tras formular la acción fundamental en los sectores electrodébil y fuerte de las teorías con derivadas con peso y de “tipo q”, hemos obtenido por primera vez cotas observacionales sobre las escalas características de la medida geométrica procedentes de la vida media del muón y del efecto Lamb shift en los átomos hidrogénicos.

Además, se ha estudiado la dimensión espectral (que indica el número de dimensiones efectivas percibidas por una partícula de prueba) en gravedades cuánticas con geometrías discretas, incluso espumas de espín, teoría de campos de grupos y gravedad de lazos. Se ha demostrado como la geometría de dichas teorías sea afectada por la estructura discreta y combinatorial de manera que la dimensión del espaciotiempo efectivo emergente de la sobreposición de estados cinemáticos cuánticos cambia con la escala y, en algunos casos, se puede declarar fractal. Este resultado permite individuar de manera precisa las escalas a partir de donde se puede definir el límite clásico.

Las teorías cuánticas de campos definidas en regiones espaciales acotadas son importantes en varias ramas de la física teórica, que van desde el estudio de los agujeros negros a los sistemas de materia condensada. Una de las características más destacadas de la relatividad general es su invariancia bajo difeomorfismos, una fuente bien conocida de dificultades conceptuales y un obstáculo serio para su cuantización consistente. Entre las ideas más populares utilizadas para entender el problema de la de invariancia bajo difeomorfismos de las teorías de campos y buscar posibles enfoques que nos acerquen a su resolución es la introducción de los llamados modelos parametrizados en los que los embeddings juegan un papel importante como variables de configuración adicionales. Éstos se pueden utilizar para evitar la introducción de foliaciones particulares y de alguna manera permiten sortear algunas de las dificultades relacionadas con el conocido problema del tiempo. La interacción entre parametrización, la presencia de fronteras espaciales y las simetrías de gauge es bastante complicada desde el punto de vista matemático y debe ser debidamente analizada con el fin de obtener la formulación hamiltoniana para estos modelos, que sirva para su cuantización. Nuestro grupo se ha concentrado en el estudio de dos tipos particulares de sistemas que de alguna manera han eludido un tratamiento satisfactorio hasta la fecha: el campo electromagnético parametrizado (para el que Kuchař y colaboradores dieron un tratamiento parcial, aunque no completamente satisfactorio) y el campo escalar parametrizado en regiones espaciales acotadas con condiciones de contorno de Dirichlet, Neumann o Robin (considerados por Marolf y colaboradores, pero, de nuevo, sólo parcialmente entendidos). Mediante el recurso a métodos hamiltonianos geométricos hemos sido capaces de obtener una formulación hamiltoniana completa y detallada para estos modelos. La característica más sorprendente e inesperada de esta descripción es la aparición de "sectores" en la hipersuperficie de ligaduras primarias. Estos sectores están asociados con el hecho de que el rango (generalizado) del pullback de la forma simpléctica a la superficie de ligaduras no es uniforme. Este fenómeno está relacionado con la aparición de una bifurcación del algoritmo de Dirac (utilizado tradicionalmente para el tratamiento de sistemas mecánicos singulares o con ligaduras). El hecho que los sistemas para los que surge esta bifurcación sean por lo general descartados como “no físicos” es una de las razones por las que no han sido estudiados en detalle y son considerados como patológicos. La circunstancia de que, modelos naturales como los que hemos discutido, muestren este tipo de comportamiento de una manera esencial justifica la necesidad de aproximarse a ellos con nuevas herramientas como las que hemos empleado. La disponibilidad de estas herramientas, puestas a punto con el estudio de los modelos mencionados anteriormente, abre la posibilidad de estudiar sistemas más complicados (relatividad general) y utilizar sus versiones parametrizadas para plantearse y entender algunas de las dificultades a las que actualmente se enfrentan los enfoques más populares para su cuantización. Nuestra esperanza es que seremos capaces de hacer frente a algunas de ellas en el futuro próximo.

Líneas de Investigación:

• Gravedad y Cosmología Cuánticas de Lazos.
• Relatividad General Clásica y Cuántica.
• Métodos computacionales en Física Gravitacional.
• Análogos de agujeros negros en Materia Condensada.
• Combinatoria.
• Teoría cuántica de campos.
• Modelos de gravedad cuántica y geometría fractal.

Labor Investigadora

Gravitación y Cosmología

El Grupo de Gravitación y Cosmología ha continuado durante 2014 su trabajo sobre la cuantización de cosmologías inhomogéneas, centrando la atención en las consecuencias que la cuantización de la geometría tiene para las perturbaciones cosmológicas y en las huellas sobre el Fondo Cósmico de Microondas. Estudiamos la evolución de un espaciotiempo homogéneo e isótropo (un espaciotiempo de Friedmann-Robertson-Walker) acoplado a un campo escalar sin masa con perturbaciones escalares pequeñas dentro del marco de la Cosmología Cuántica de Campos, usando una propuesta para la dinámica efectiva que se basa en una cuantización híbrida que previamente habíamos logrado nosotros. Introdujimos una fijación de gauge conveniente y adoptamos variables canónicas reducidas adaptadas a esa descripción cuántica híbrida. Además, mantuvimos las contribuciones de backreaction sobre el fondo (background) procedentes de los términos de la acción del sistema cuadráticos en las perturbaciones. Llevamos a cabo un análisis numérico asumiendo que las inhomogeneidades estaban inicialmente (en el pasado distante) en un vacío sin masa. En el futuro distante, observamos una amplificación estadística de la amplitud de los modos en la región infrarroja, así como una sincronización de las fases debida a fenómenos de gravedad cuántica. Finalmente, analizamos algunas consecuencias de la backreaction en nuestra descripción efectiva.

También estudiamos perturbaciones cosmológicas en el marco de la Cosmología Cuántica de Lazos usando variables de Mukhanov-Sasaki en el formalismo de cuantización híbrida. La formulación en términos de estos invariantes de gauge permite clarificar la independencia de los resultados en elecciones de gauge y facilita la comparación con otros formalismos propuestos para tratar las perturbaciones cosmológicas en el contexto de la Teoría Cuántica de Lazos. Empleamos un tipo de aproximación de Born-Oppenheimer para extraer la dinámica de las perturbaciones, separándolas de los grados de libertad de la geometría de Friedmann-Robertson-Walker. Con esta aproximación, dedujimos una ecuación de Schrödinger para las perturbaciones cosmológicas y estudiamos su rango de validez. Asimismo, probamos que, con un orden de factores diferente, la dinámica de las perturbaciones que se obtenía era similar a la encontrada en el llamado formalismo de “métrica vestida”, salvo por un posible escalado del campo material para garantizar la unitariedad de su evolución en el régimen de Teoría Cuántica de Campos en un espaciotiempo curvo, y aparte de algunas cuestiones de prescripciones de la cuantización. Finalmente, calculamos las ecuaciones effectivas que resultan gobernar las variables de Mukhanov-Sasaki, tanto con la aproximación de Born-Oppenheimer como sin ella.

Además de todo esto, y para poder contemplar la posibilidad de cambios de signatura en la geometría cuántica, estudiamos la cuantización de campos escalares de tipo Klein-Gordon en espaciotiempos no estacionarios, como los que se encuentran en cosmología, suponiendo que toda la dependencia espacial relevante para las ecuaciones de campo estaba contenida en el laplaciano. Mostramos que la descripción de campo y la representación de Fock para la cuantización del campo quedan fijadas de forma única (salvo por transformaciones unitarias que no afectan las predicciones físicas) si se adopta un criterio combinado de (a) imponer la invariancia del vacío bajo el grupo de simetrías espaciales de las ecuaciones de campo y (b) requerir una implementación unitaria de la dinámica en la teoría cuántica. También proporcionamos una interpretación espaciotemporal de las ecuaciones de campo como las correspondientes a un campo escalar en un espaciotiempo cosmológico que es conformemente ultraestático. En la cuantización de Fock privilegiada, investigamos la generalización de la evolución de los estados físicos desde el régimen de dinámica hiperbólica a un régimen elíptico, debido a procesos con cambio de signatura en el espaciotiempo en el que se propaga el campo. Discutimos el comportamiento de la geometría de fondo cuando ocurre el cambio, y probamos que la métrica del espaciotiempo degenera totalmente. Finalmente, mostramos que este tipo de cambio de signatura conduce de forma natural a un fenómeno de creación de partículas, con una producción exponencial.

En nuestro estudio de inhomogeneidades en Cosmología Cuántica de Lazos, por otra parte, también desarrolamos métodos aproximados en la cuantización híbrida del modelo de Gowdy con polarización lineal y un campo escalar sin masa, para el caso de una topología espacial toroidal en tres dimensiones. Los modelos de Gowdy son espaciotiempos cosmológicos inhomogéneos con simetrías que simplifican el análisis. La Cuantización de Lazos del sector gravitatorio homogéneo del modelo de Gowdy y la presencia de inhomogeneidades conducen a una ligadura hamiltoniana muy complicada. Por tanto, la extracción de resultados físicos reclama la introducción de aproximaciones bien justificadas. Primero mostramos cómo aproximar la parte homogénea de la ligadura hamiltoniana, correspondiente a geometrías anisótropas de tipo Bianchi I, como si se trataran de un modelo isótropo de Friedmann-Robertson-Walker corregido con anisotropías. Esta aproximación es válida en el sector de altas energías de la geometría de Friedmann-Robertson-Walker y cuando la función de ondas de las anisotropías es suficientemente suave. Además, para ciertas familias de estados relacionados con regímenes de interés físico, con efectos cuánticos de las anisotropías despreciables e inhomogeneidades pequeñas, es posible aproximar la ligadura hamiltoniana del sistema por el de una geometría de Friedmann-Robertson-Walker con un contenido material simple, y así obtener soluciones aproximadas.

Por otra parte, hemos discutido también el problema de la existencia de correlaciones cuánticas en la geometría más allá de horizontes gravitatorios. Clásicamente, regiones diferentes del espaciotiempo que están separadas por horizontes no se relacionan entre sí. Llevamos a cabo una cuantización canónica de un modelo de tipo Kantowski- Sachs cuyas soluciones clásicas exhiben tanto un horizonte de sucesos como uno cosmológico, para comprobar así si la afirmación anterior sobre regiones separadas por horizontes se mantenía desde el punto de vista cuántico. Nuestro análisis mostró que, en realidad, no sucede así. Estado gravitatorios cuánticos con soporte en configuraciones espaciotemporales que describen exclusivamente bien la región entre horizontes, bien la región externa, no son consistentes en tanto en cuanto resultan conectarse entre sí mediante operadores unitarios que describen una noción natural de evolución.

También hemos dado una descripción detallada de la electrodinámica como una teoría emergente a partir de estructuras similares a las que aparecen en materia condensada, no solo por su interés intrínseco sino también como preparación para el estudio mucho más complejo de la gravedad. Comenzamos con el modelo mecánico de Maxwell para la electrodinámica. A continuación tomamos un sistema similar al helio 3 superfluido como representante de una clase amplia de sistemas cuánticos fermiónicos cuya física de baja energía reproduce la electrodinámica clásica.

El sector de agujero blanco de la solución de Kruskal casi nunca se utiliza en aplicaciones físicas. Sin embargo, podría contener la solución a muchos de los problemas asociados con el colapso gravitatorio y la evaporación subsiguiente. Existen geometrías de rebote que hacen un uso democrático de los sectores de agujero negro y de agujero blanco. Estos comportamientos podrían ser naturales en el siguiente nivel más allá de la relatividad general.

En otro ámbito de cuestiones, se acepta comúnmente que la relatividad general en la única solución al problema de consistencia en la construcción de una teoría de gravitones (partículas de espín 2 sin masa) en interacción. Presentamos el problema de autoacoplo en detalle y lo resolvimos explícitamente para la teoría más simple. Hicimos explícito el problema de la no unicidad y mostramos que la única teoría resultante que implementa una deformación de la simetría gauge original tiene esencialmente la misma estructura que la gravedad unimodular, lo que permite pensar en una solución natural para el primer problema de la constante cosmológica en teorías de gravedad emergente. Después analizamos la teoría de Fierz-Pauli theory (equivalente pero con más simetría gauge). Mediante el requisito de que se preserve una deformación de la simetría gauge interna, se recupera naturalmente la estructura de la gravedad unimodular de la relatividad general pero en una versión que exhibe la estructura minkowskiana subyacente (al estilo de la teoría bimétrica de Rosen).

Una de las características más peculiares de la cuantización utilizada en la Gravedad Cuántica de Lazos es la no-separabilidad de los espacios de Hilbert utilizados. Se espera que esto no sea un problema en la formulación final de la gravedad cuántica porque los espacios físicos de Hilbert determinados por las soluciones a las ligaduras cuánticas serán, muy probablemente, separables. En cualquier caso, hay una serie de cuestiones que no han sido contestadas de manera completamente satisfactoria y que, por lo tanto, es interesante abordar: en particular, la mecánica estadística de estos modelos, la superselección de ciertos espacios de Hilbert y la caracterización de las ambigüedades introducidas por la escala polimérica. Un entorno natural para estudiar estas cuestiones es el proporcionado por la denominada mecánica cuántica polimérica, que incorpora algunas de las características más singulares de la cuantización de la relatividad general que nos da la GCL y es especialmente relevante para la Cosmología Cuántica de Lazos. En los últimos años hemos prestado atención al estudio de los sistemas simples, como el oscilador armónico polimerizado en una dimensión, con la esperanza de lograr una buena comprensión de la no-separabilidad. En el último año hemos considerado, en colaboración con el Dr. Tomasz Pawlowski —antiguo miembro del grupo— la extensión de algunos de nuestros resultados al estudio de modelos en cosmología cuántica. La idea clave ha sido la de sustituir los espacios no separables por otros separables, con medidas adecuadas sobre el espectro de los operadores relevantes para definir observables cuánticos. Aunque esta idea puede ser finalmente demasiado sencilla, es bastante útil para entender no separabilidad y cuestiones relacionadas con superselección.

El trabajo llevado a cabo por el grupo sobre entropía de agujeros negros en LQG durante los últimos años llevó al desarrollo de varias herramientas matemáticas necesarias para resolver los problemas combinatorios involucrados en el cálculo de la entropía. Un resultado de tipo matemático que ha tenido su origen en esos trabajos nos ha llevado a la resolución de un antiguo problema de combinatoria que aparece formulado en el famoso libro Concrete Mathematics de Graham, Knuth y Patashnik. El problema en cuestión pide resolver y caracterizar las soluciones a una recurrencia lineal de seis parámetros muy general cuyas soluciones incluyen a grandes familias de números combinatorios conocidos; entre ellos los coeficientes binomiales, los números de Stirling, los números de Euler y muchos otros. La resolución de este problema se ha basado en el uso de funciones generatrices de dos variables similares a las utilizadas por el grupo para estudiar los agujeros negros. Un descubrimiento sorprendente ha sido la identificación de un fenómeno que es natural denominar invariancia de gauge y que consiste en la existencia de diferentes conjuntos de parámetros que conducen a las mismas familias de números combinatorios. El trabajo ha sido publicado en la prestigiosa revista Journal of combinatorial Theory, Series A y ha dado lugar a un nuevo trabajo sobre las aplicaciones del formalismo que hemos desarrollado (enviado a publicar al Electronic Journal of Combinatorics).

Un problema importante sugerido también por la actividad del grupo en física de agujeros negros es el estudio riguroso de la formulación hamiltoniana para teorías de campos en la presencia de fronteras. Recuérdese que el modelo utilizado actualmente para describir los agujeros negros en el marco de la GCL se basa en la utilización de los llamados horizontes aislados y la formulación de la relatividad general en regiones de espacio-tiempo con fronteras interiores. El origen de los grados de libertad cuánticos que dan cuenta de la entropía es algo misterioso y, en particular, la relación entre los grados de libertad clásicos y cuánticos no está completamente clara. Con el objetivo de aclarar este tema y alcanzar una comprensión rigurosa de la relatividad general en presencia de fronteras espacio-temporales hemos comenzado a estudiar la formulación hamiltoniana rigurosa para teorías de campos en regiones espaciales acotadas. Uno de los objetivos de este trabajo ha sido el de caracterizar aquéllas teorías de campos para las que aparecen de forma natural grados de libertad asociados con fronteras. El primer trabajo sobre este tema, publicado en Classical and Quantum Gravity y distinguido como highlight del año 2014 por esta prestigiosa revista, trata sobre al estudio de campos escalares y electromagnéticos en regiones acotadas con fronteras suaves y determinadas por condiciones de contorno de distintos tipos (Dirichlet, Neumann, Robin y otras específicas del campo EM). En estos ejemplos hemos sido capaces de demostrar rigurosamente que no aparecen grados de libertad en las fronteras. En este momento estamos extendiendo los resultados de este trabajo al estudio del campo escalar parametrizado y a modelos de campos acoplados a partículas puntuales. Estos trabajos —en curso o en proceso de publicación— arrojarán más luz sobre la cuestión de la existencia de auténticos grados de libertad asociados a fronteras espaciotemporales y la entropía de los agujeros negros.

Dentro del marco de cosmología cuántica de lazos, se ha estudiado la posibilidad de obtener las ecuaciones homogéneas de LQC a partir de la teoría de campos de grupo, una teoría independiente del fondo y supuestamente más fundamental que la gravedad de lazos. En este caso, se ha usado un estado condensado cuántico para reproducir un fondo cosmológico en el límite continuo. Hemos también explorado otras teorías de gravedad cuántica, donde se ha hecho hincapié sobre el cambio de propiedades de la geometría efectiva al variar de la resolución. (i) En la teoría de gravedad no-local propuesta por G. Calcagni and L. Modesto, se ha construido una lagrangiana de gravedad in 11 dimensiones con operadores no-locales y que reproduce varias características de la teoría M y de campos de cuerdas. Con respecto a la cosmología, se ha mostrado que es posible remplazar la singularidad del big bang con un rebote clásico, por efecto de los operadores no-locales. Hemos también discutido la misma no-localidad de dichos modelos en teoría de cuerdas. (ii) Se han desarrollado la electrodinámica (clásica y cuántica) y la cosmología de espaciotiempos multi-escala, teorías recién propuestas donde la geometría cambia con la escala de manera similar a las de multi-fractales. La medida geométrica produce naturalmente un periodo de contracciones y expansiones cíclicas que puede dejar una huella única en los espectros de inflación primordial. La constante cosmológica que domina el universo reciente se reinterpreta como un “potencial” efectivo generado por la medida geométrica, necesario para la auto consistencia de las soluciones. (iii) Se han puesto cotas observacionales sobre modelos cosmológicos de geometría no-conmutativa, de brana y de tunneling cuántico, logrando excluir experimentalmente las primeras dos clases gracias a los datos de Planck. (iv) Se ha empezado el estudio de la dimensión espectral (que indica el número de dimensiones efectivas percibidas por una partícula de prueba) en gravedades cuánticas con geometrías discretas, incluso espumas de spin y gravedad de lazos.

Por último, en el cluster Trueno hemos instalado y comprobado con éxito el programa FORTRAN CosmoMC de simulaciones de Monte Carlo cosmológicas. CosmoMC es un instrumento fundamental para poner cotas observacionales sobre modelos teóricos del universo primitivo y nos permitirá verificar experimentalmente y directamente las predicciones inflacionarias de muchos de los modelos aquí discutidos. El IEM-CSIC se convierte así en el primer nodo nacional equipado con este importante código de cosmología numérica.

Líneas de Investigación:

• Gravedad y Cosmología Cuánticas de Lazos.
• Relatividad General Clásica y Cuántica.
• Análogos de agujeros negros en Materia Condensada.

Labor Investigadora

Gravitación y Cosmología

Durante 2013 hemos continuado con el estudio de cosmologías inhomogéneas en el marco de la Cosmología Cuántica de Lazos, prestando especial atención al tratamiento de perturbaciones cosmológicas alrededor de universos homogéneos e isotrópos como éste en el que vivimos, en primera aproximación. Más específicamente, hemos presentado una cuantización completa de un universo aproximadamente homogéneo e isótropo con pequeñas perturbaciones escalares en el caso en el que el contenido de materia es un campo escalar mínimamente acoplado y las secciones espaciales son planas y compactas. La cuantización se ha llevado a cabo siguiendo las líneas desarrolladas por nuestro grupo en trabajos previos para topología esférica. Hemos truncado la acción del sistema a segundo orden en las perturbaciones, y fijado la libertad de gauge local en el nivel clásico, aunque hemos estudiado diferentes gauges y demostrado que con todos ellos se infieren conclusiones equivalentes. Por otra parte, hemos considerado también descripciones en términos de cantidades invariante de gauge. Hemos demostrado que el sistema obtenido por reducción de esta manera admite una estructura simpléctica, y su evolución dinámica está dictada por una ligadura hamiltoniana. A continuación, hemos procedido a cuantizar la geometría de fondo con técnicas de lazos, a la vez que hemos adoptado una representación de Fock para las inhomogeneidades. Esta última representación ha sido seleccionada por criterios de unicidad propuestos por nuestro grupo en el contexto de teoría cuántica de campos en espacio-tiempos curvos. Estos criterios determinan también un escalado particular de las perturbaciones. En nuestra cuantización híbrida, que combina métodos de lazos y de Fock, hemos representado la ligadura hamiltoniana como un operador en el espacio de Hilbert cinemático. Si se impone esta ligadura, y si el modo cero del campo escalar se interpreta como un tiempo relacional, un ansatz adecuado para la dependencia de los estados físicos en los grados de libertad de lazos conduce a una ecuación de onda cuántica para la evolución de las perturbaciones. Alternativamente, las soluciones a la ligadura cuántica se pueden caracterizar por sus datos iniciales sobre una sección de volumen mínimo. Las consecuencias físicas de este modelo se están discutiendo en la actualidad, con el fin de comprobar si son compatibles con las observaciones cosmológicas.

Un punto importante en nuestra cuantización híbrida es la posibilidad de seleccionar una representación de Fock única para los campos perturbativos mediante ciertos criterios que nuestro grupo ha introducido en los últimos años. Estos criterios consisten en los requisitos de (i) la invariancia del vacío bajo las simetrías espaciales de las ecuaciones de campo y (ii) la aplicabilidad de la dinámica como una transformación unitaria en la teoría cuántica. En el caso de perturbaciones cosmológicas, los campos que describen las inhomogeneidades pasan por un período inflacionario que puede ser entendido como la propagación en un fondo de Sitter. Con esta motivación, hemos demostrado que, bajo el escalado conforme estándar utilizado en cosmología, un campo sin masa en el espaciotiempo de Sitter admite una cuantización de Fock O (4)-invariante tal que la evolución temporal se implementa efectivamente de forma unitaria, y además que esta cuantización es esencialmente única. Este resultado refuta afirmaciones aparecidas anteriormente en la literatura. También hemos discutido la relación entre esta cuantización privilegiada con dinámica unitaria y la basada en la familia de estados invariantes O(4) de tipo Hadamard dados por Allen y Folacci, así como con la que se basa en el vacío de Bunch-Davies, habitual en cosmología inflacionaria.

Por otra parte , hemos demostrado la solidez de los criterios para la selección de una cuantización de Fock única de campos escalares de tipo Klein-Gordon en escenarios no estacionarios con secciones espaciales compactas, permitiendo también diferentes descripciones de los campos que se relacionan por medio de ciertas transformaciones canónicas lineales y no locales. Más concretamente, hemos considerado transformaciones que no mezclan modos propios del operador de Laplace-Beltrami, que se supone que están desacoplados de forma dinámica. Transformaciones canónicas de este tipo se encuentran en el estudio de las perturbaciones escalares en cosmologías inflacionarias, al relacionar, por ejemplo, los grados de libertad física de estas perturbaciones después de una fijación de gauge con cantidades invariantes de gauge. Por lo tanto, nuestros resultados tienen implicaciones inmediatas para nuestra cuantización híbrida de las perturbaciones escalares en Cosmología Cuántica de Lazos. Hemos caracterizado todas las posibles transformaciones del tipo considerado y hemos mostrado que, independientemente de la descripción inicial de campo, nuestros criterios de invariancia bajo la simetría espacial y de una dinámica unitaria conducen de hecho a una cuantización de Fock única, módulo transformaciones unitarias que no afectan a las predicciones físicas.

Otra de las cuestiones que hemos analizado en detalle en el contexto de la Cosmología Cuántica de Lazos es la resolución de singularidades. Recordemos que uno de los fenómenos más notables de la Cosmología Cuántica de Lazos es que, al menos para los modelos cosmológicos homogéneos, el Big Bang se reemplaza con un Big Bounce que conecta nuestro universo con una rama anterior sin pasar por una singularidad cosmológica. Por primera vez en la literatura, hemos estudiado la existencia de singularidades en Cosmología Cuántica de Lazos incluyendo inhomogeneidades, y hemos comprobado que el comportamiento obtenido en el caso puramente homogéneo sigue siendo válido. Hemos centrado nuestra atención en las cosmologías de Gowdy con ondas gravitacionales linealmente polarizadas y hemos utilizado dinámica efectiva para llevar a cabo el análisis. Para el modelo cosmológico considerado, hemos demostrado que todas las posibles singularidades cosmológicas se evitan por los efectos de la cuantiación de lazos, logrando así una generalización de los resultados acerca de la resolución de singularidades a este escenario con falta de homogeneidad. También hemos probado que, si se produce un rebote en el volumen (del fondo homogéneo), las inhomogeneidades aumentan el valor de ese volumen en el rebote.

Asimismo, hemos identificado huellas de efectos cuánticos gravitatorios que sobreviven desde el universo primitivo hasta la época actual: las fluctuaciones de los campos cuánticos vistos por observadores comóviles son sensibles a la historia del universo primitivo. La existencia (o no) de un rebote cuántico deja una traza en el ruido cuántico de fondo que no se atenúa y que no sería despreciable, ni siquiera hoy. Hemos estimado una cota superior a la energía típica a la que los efectos cuánticos son relevantes. También hemos presentado el problema de autoacoplo de gravitones en detalle y hemos resuelto el problema de infinitas interacciones asociado, complementando así resultados previos referentes a la recuperación de la Relatividad General en este esquema. Hemos concluido que, mientras se requiera la preservación de la invariancia gauge, se recupera de forma natural la estructura de la Relatividad General, pero en una versión que muestra explícitamente un espaciotiempo minkowskiano de fondo al estilo de Rosen.

Durante este último año, por otra parte, también hemos desarrollado líneas de investigación de geometría cuántica y anómala. Gianluca Calcagni ha dedicado todo el 2013 a consolidar una clase de modelos de espaciotiempos multiescala donde la geometría del universo tiene las propiedades típicas de los multi-fractales. Los objetivos han sido: 1) desarrollar una teoría coherente que pueda explicar analíticamente algunas características universales de espaciotiempos que aparecen en muchos modelos independientes de gravedad cuántica, 2) desarrollar su fenomenología, especialmente la de teoría clásica y cuántica de campos y de cosmología, 3) verificar su viabilidad experimental. Los objetivos 1) y 2) han sido alcanzados totalmente y hemos aclarado mucho la estructura fundamental de estas geometrías, sus propiedades en presencia de una curvatura métrica y sus consecuencias cosmológicas para el universo primigenio y la constante cosmológica, mientras que 3) está todavía en fase de estudio. En paralelo, Calcagni ha trabajado sobre cosmologías de universo de brana y no-conmutativos y sobre geometrías anómalas y el cálculo de la dimensión espectral en varios enfoques, incluidos teoría de cuerdas, “asymptotic safety”, agujeros negros, gravedad cuántica de lazos y una teoría super-renormalizable de gravedad cuántica propuesta por L. Modesto y otros, para la cual hemos encontrado soluciones cosmológicas con rebote.

Dentro del estudio de aspectos generales sobre teoría cuántica de campos se ha dedicado especial atención al estudio del formalismo hamiltoniano para modelos definidos en regiones espaciales acotadas. La importancia inmediata de estos modelos en el contexto de la gravedad cuántica reside en el hecho de que el tratamiento habitual de los agujeros negros en Gravedad Cuántica de Lazos se lleva a cabo mediante la introducción de horizontes aislados; un tipo de fronteras interiores para el espacio tiempo en las que se imponen condiciones de contorno naturales que dan lugar a un tipo de horizonte casi-local. El problema principal que se presenta a la hora de tratar estos sistemas es el de la interpretación de estas condiciones sobre la frontera, en particular averiguar si se trata de ligaduras en el sentido habitual y su tipo (primera o segunda clase) –del que depende críticamente su tratamiento cuántico.

Desde un punto de vista técnico la presencia de fronteras nos obliga a utilizar un esquema matemático más elaborado que el que se obtiene al generalizar de manera formal el método tradicional de Dirac utilizado para el estudio de sistemas lagrangianos singulares. El contexto apropiado para el estudio de este tipo de sistemas en presencia de fronteras viene dado por los métodos geométricos desarrollados para este fin por Gotay, Nester y Hinds. Estos autores desarrollaron un esquema geométrico preciso (que para el caso particular del estudio de teorías de campos se apoya en el uso de variedades diferenciales de dimensión infinita modeladas sobre espacios de Banach) que se adapta perfectamente al tipo de problemas que nos interesa. Hay que señalar que desde el punto de vista técnico el trabajo con variedades de dimensión infinita requiere del uso de técnicas de análisis funcional que introducen importantes dificultades matemáticas.

Durante el año 2013 se ha conseguido poner en marcha un ambicioso programa de trabajo sobre este tema que se ha materializado en el estudio completo y sistemático de modelos de campos escalares con diversas condiciones de contorno (de tipo Dirichlet y Robin) y de campos de Maxwell (con condiciones de tipo conductor perfecto y Neumann). El trabajo realizado ha dado lugar a una publicación en Classical and Quantum Gravity (en colaboración con Jorge Prieto y Eduardo Sánchez Villaseñor) que ha aparecido en enero de 2014. En el momento actual se están extendiendo los resultados obtenidos a modelos en interacción (campos escalares y Yang-Mills) y modelos en los que se espera que de forma natural haya grados de libertad físicos asociados a las fronteras (Maxwell-Chern-Simons en 2+1 dimensiones).

Dentro del contexto de la Gravedad Cuántica de Lazos y la Cosmología Cuántica de Lazos es importante entender las consecuencias físicas de la introducción de espacios de Hilbert no separables. Para ello se han considerado en la literatura diversos tipos de modelos, en particular el oscilador armónico polimérico, y se han estudiado algunas características del espectro de la versión polimérica del hamiltoniano. Durante el año pasado conseguimos una caracterización precisa de este. El resultado más importante que obtuvimos fue determinar que el espectro genérico de los hamiltonianos poliméricos para el oscilador es un espectro de bandas (como el de los sólidos) pero puramente puntual (y por tanto asociado a verdaderos autovalores). Los resultados obtenidos han dado lugar a una publicación en Classical and Quantum Gravity (en colaboración con Jorge Prieto y Eduardo Sánchez Villaseñor). En el momento presente estamos explorando las consecuencias de los resultados obtenidos en Cosmología Cuántica de Lazos así como proponiendo alternativas a los espacios de Hilbert no separables de uso habitual.

Finalmente se ha dedicado un esfuerzo considerable al estudio de problemas combinatorios utilizando los métodos de funciones generatrices puestos a punto durante los últimos años en el estudio de la entropía de agujeros negros en Gravedad Cuántica de Lazos. El trabajo realizado se ha concentrado en el estudio completo de una importante clase de recurrencias lineales que generaliza a las que definen importantes familias de números combinatorios que incluyen a los números de Euler, Stirling, Ward, Lah etc. Ha dado lugar a dos trabajos (en colaboración con Jesús Salas y Eduardo Sánchez Villaseñor de la Universidad Carlos III de Madrid) que se encuentran sometidos al lento proceso de revisión propio de las revistas de matemáticas (Journal of Combinatorial Theory, Series A).

Líneas de Investigación:

• Gravedad y Comología Cuántica de lazos.
• Relatividad General Clásica y Cuántica.
• Métodos computacionales en Física Gravitacional.
• Análogos de agujeros negros en Materia Condensada.

Labor Investigadora

Gravitación

El Grupo de Gravitación y Cosmología ha continuado durante este año su labor investigadora de los efectos de las inhomogeneidades en Cosmología Cuántica. Esta labor se ha desarrollado en dos frentes. Por un lado, se ha realizado un estudio pormenorizado de la cuantización de campos escalares en espaciotiempos curvos no estacionarios, situación genérica en cosmología. Este estudio ha llevado a obtener potentes teoremas sobre la unicidad de la cuantización cuando se imponen dos requisitos bastante naturales: por un lado, que el vacío de la teoría sea invariante bajo las simetrías espaciales de las ecuaciones de campo; por otro, que la dinámica cuántica sea unitaria, para preservar la interpretación convencional de la Mecánica Cuántica. Se ha estudiado con especial detalle el caso de espaciotiempos con secciones compactas de topología plana, por su interés físico, ya que las observaciones actuales del Universo apuntan a su planitud espacial. Así, se ha demostrado la unicidad tanto de la representación de Fock empleada en la cuantización, como de la elección de un par canónico para el campo cuando se permiten transformaciones canónicas dependientes del tiempo en el sistema. Es natural considerar estas transformaciones en fondos no estacionarios. Su inclusión modifica la dinámica, y conllevaría una ambigüedad en la descripción seleccionada para el campo de no ser por los resultados de unicidad mencionados.

Las conclusiones alcanzadas en el caso de topología plana han sido extendidas luego para cualquier topología espacial compacta, alcanzando conclusiones de una generalidad destacable. Estos teoremas de unicidad dan fortaleza a las predicciones físicas de la teoría, que de otra forma estarían plagadas de una ambigüedad infinita. Dentro del ámbito de campos en espaciotiempos curvos no estacionarios, se ha desarrollado también un formalismo teórico para la descripción de perturbaciones cosmológicas en modelos de tipo Bianchi III y libres de cizalladura. Este formalismo permite afrontar el estudio de perturbaciones primordiales en escenarios con anisotropía y discutir las posibles consecuencias observacionales, estudio de alto interés dadas las recientes indicaciones de que podrían existir ejes privilegiados en cosmología.

Asimismo, se ha estudiado la teoría de perturbaciones cosmológicas en espacios isótropos y homogéneos, convencionales en cosmología, aplicando los resultados del Grupo sobre la unicidad de la cuantización de Fock a tales perturbaciones. Aún más, se ha combinado esta cuantización de Fock privilegiada con la cuantización del fondo homogéneo e isótropo mediante técnicas de lazos, dentro del marco de la Cosmología Cuántica de Lazos (Loops). Esta técnica de cuantización híbrida, desarrollada por el Grupo del IEM, ha permitido un modelo cuántico completo y consistente para la descripción de perturbaciones primordiales en un Universo con un contenido material proporcionado por un campo escalar masivo, para el que se sabe que existen regímenes en los que se genera suficiente inflación, proporcionando así un escenario físicamente realista.

Continuando con aspectos relacionados con teoría cuántica de campos en espacios curvos, se han comparado explícitamente las estructuras del tensor de energía-momento renomalizado de un campo escalar sin masa en un espaciotiempo unidimensional obtenidas mediante dos estrategias diferentes: la construcción de modos normales del operador campo y la acción efectiva a un loop. Así, se ha visto que estos dos esquemas dan los mismos resultados mediante la correspondencia adecuada. También se han revisado algunos de los modelos de cuantización con formalismos híbridos propuestos en la literatura, con el objetivo de extraer sus características comunes. En particular, se ha visto que esos formalismos requieren en general tener en cuenta grados de libertad adicionales a los esperados en una cuantización directa del sistema.

Por otro lado, se ha analizado el entrelazamiento cuántico de un estado inicial de un campo en un espaciotiempo de colapso gravitatorio y se ha discutido el tipo de problemas que se pueden discutir con el formalismo presentado, así como las posibles líneas de investigación futura. Desde otro punto de vista, un estado de vacío en un agujero negro puede analizarse en términos de cómo se percibe por distintos observadores mediante el uso de una función de temperatura efectiva. Se ha encontrado una expresión analítica general para esta temperatura, que depende del estado de vacío, de la posición, de la velocidad local y de la aceleración del observador en cuestión. También se ha proporcionado una interpretación física de las distintas cantidades que aparecen en dicha expresión e ilustrado su interés con algunos ejemplos.

Otra línea de investigación desarrollada ha sido la referente a espaciotiempos cuánticos efectivos con geometría multifractal, cuyas propiedades cambian al variar de la escala observacional. Los objetivos principales consisten en construir una teoría auto-consistente de dinámica cuántica de campos y hallar sus propiedades de re normalización, y con ello desarrollar un formalismo de gravedad clásica en espaciotiempos multifractales, para estudiar escenarios cosmológicos y su fenomenología.

En cuanto al estudio de la entropía de los agujeros negros en Gravedad Cuántica de Lazos, se ha comenzado un programa de estudio riguroso de las teorías cuánticas de campos en presencia de fronteras, concentrado especialmente en su tratamiento Hamiltoniano. Uno de los problemas conceptuales más importantes en este aspecto es el relacionado con la interpretación de los grados de libertad a cuya existencia se atribuye la aparición de la entropía. Los agujeros negros en GCL se modelizan mediante la introducción de los llamados horizontes aislados. En el momento presente se interpreta que, desde el punto de vista clásico no hay grados de libertad que puedan ser asignados de manera exclusiva a la frontera y que, por tanto, los grados de libertad que dan cuenta de la entropía tienen que tener, por fuerza, un origen puramente cuántico. El problema con este punto de vista es que la identificación de los grados de libertad clásicos requiere de un tratamiento Hamiltoniano riguroso, que incorpore en particular los aspectos necesarios relacionados con los espacios funcionales a los que pertenecen los campos clásicos. Para lograr este objetivo no bastan los métodos basados en el algoritmo de Dirac tradicional sino que es necesario recurrir a métodos geométricos adaptados al carácter infinito-dimensional de los espacios de configuración de las teorías de campos. Entre estos métodos hay que destacar el algoritmo geométrico de Gotay-Nester-Hinds. En un primer paso se ha utilizado este formalismo para describir teorías lineales con fronteras, con el objetivo de determinar si las condiciones de contorno admiten una interpretación como ligaduras en el sentido tradicional. Los modelos considerados hasta la fecha han sido los campos escalares y electromagnético con condiciones de contorno de tipo Dirichlet y Robin y se han caracterizado completamente las variedades diferenciales de ligadura en las que se desarrolla la dinámica junto con la descripción precisa de los Camps de vectores Hamiltonianos. Para ello ha sido necesario encontrar el tipo de espacios funcionales apropiados (espacios de Sobolev asociados a los distintos operadores diferenciales que aparecen). En el momento actual se están extendiendo estos resultados a teorías parametrizadas para poder entender en detalle aspectos asociados con su cuantización polimérica.

Líneas de Investigación:

• Relatividad General Clásica y Cuántica.
• Cosmología Cuántica.
• Gravedad Cuántica de Lazos
• Análogos de agujeros negros en Materia Condensada.
• Física de agujeros negros.

Labor Investigadora

Gravedad Cuántica y Cosmología Cuántica

Durante el año 2011 hemos completado el trabajo llevado a cabo durante los últimos años sobre el estudio de la entropía de los agujeros negros en el formalismo de la gravedad cuántica de lazos (GCL). En concreto hemos podido concluir los estudios relativos al comportamiento asintótico de la entropía como una función del área del horizonte. El problema abierto más importante que quedaba por resolver era averiguar si la estructura observada en el régimen de áreas pequeñas estaba presente también en el régimen asintótico. Para ello, durante el año 2010 desarrollamos una serie de métodos estadísticos que permitieron definir un procedimiento de aproximación para la entropía de conteo que explicaba la desaparición de la referida estructura a grandes escalas. El resultado descrito anteriormente puede ser entendido desde una perspectiva completamente distinta si recurrimos al formalismo de la mecánica estadística y, en particular, a algunos aspectos relacionados con su fundamentación matemática. En este contexto se plantea el estudio de las propiedades matemáticas de la entropía de cualquier sistema físico como función de la energía (la variable relevante para la física estadística ordinaria). En particular es especialmente importante determinar bajo qué circunstancias la entropía es una función suficientemente suave de la energía y sus propiedades de concavidad y convexidad. El primer punto es relevante porque las magnitudes termodinámicas (por ejemplo la temperatura de un sistema) están definidas como derivadas de la entropía mientras que el segundo punto es central para la comprensión de la estabilidad de los sistemas físicos. Lo que demuestran los teoremas clásicos es que en el llamado límite termodinámico la entropía satisface condiciones razonables de suavidad y concavidad.

Durante el año pasado hemos dedicado un esfuerzo considerable a entender, aprovechando las técnicas combinatorias que hemos desarrollado en los últimos años para el estudio de agujeros negros, el problema del límite termodinámico para este tipo de sistemas. Dado que en nuestro caso es posible describir de manera efectiva tanto la colectividad microcanónica (de área) como la canónica, hemos podido estudiar lo que sucede con los agujeros negros en este límite (que no ha de ser confundido con el de grandes áreas). La conclusión más importante de nuestros trabajos es que, en el límite termodinámico, la entropía de los agujeros negros que hemos estudiado es una función del área, suave, cóncava y con un comportamiento compatible con la ley de Bekenstein-Hawking que establece una relación lineal entre entropía y área. Hay que destacar, sin embargo, el hecho de que las correcciones subdominantes para la entropía termodinámica (logarítmicas en el área) no coinciden con las de la entropía de conteo o estadística. Este hecho ha de ser relevante no solo en el contexto de la GCL sino también en otros esquemas que se ocupan de este tipo de problemas, en particular, las teorías de cuerdas.

Hemos empleado también métodos de GCL para analizar la vertiente cuántica en sistemas cosmológicos, en el campo de especialización que se conoce hoy en día como cosmología cuántica de lazos (CCL). En particular, durante 2011 hemos implementado y comparado las llamadas prescripciones de dinámica mejorada que existen en la literatura, estudiando espaciotiempos homogéneos e isótropos que contienen un campo escalar sin masa. Hemos comprobado que todas estas prescripciones conducen a los mismos resultados cualitativos para estados semiclásicos en dichos espciotiempos cosmológicos, y que el comportamiento físico es similar en realidad incluso para estados que no son tan semiclásicos o en regímenes donde los efectos cuánticos empiezan a no ser totalmente despreciables, pero existen diferencias. Lo que es más importante, no todas estas prescripciones tienen las mismas propiedades desde el punto de vista de las simulaciones numéricas. En concreto, una prescripción introducida por nosotros parece ser especialmente sencilla de implementar y reduce considerablemente el tiempo de cómputo. Hemos optimizado los códigos de nuestra librería numérica para simulaciones en CCL, con objeto de aprovechar plenamente las características de esta prescripción específica. .

Durante este año también hemos aplicado técnicas de lazos a cosmologías inhomogéneas del tipo Gowdy y que incuyen un campo escalar sin masa, alcanzando por vez primera una cuantización completa y consistente en el marco de la CCL para un modelo con grados de libertad locales en el contenido material y en la geometría. Hemos desarrollado una propuesta para la cuantización híbrida de este modelo, y lo hemos implementado completamente, probando la consistencia de nuestra construcción. El objetivo de este trabajo ha sido multiple: a) obtener una descripción cuántica exacta de cosmologías inhomogéneas con campos materials que incluyan efectos de geometría cuántica de lazos, b) determinar el espacio de estados físicos y un conjunto completo de observables físicos, c) probar que la dinámica cuántica está bien puesta, d) demostrar que las singularidades cosológicas se resuelven en este marco, y e) mostrar que uno recupera la cuantización de Fock estándar para las inhomogeneidades en regímenes apropiados para estados físicos. Más aún, restringiendo el análisis al caso vacío, hemos discutido también el efecto de las inhomogeneidades en el Big Bounce que remplaza la singularidad de Big Bang, usando la teoría efectiva asociada a nuestro modelo cuántico exacto. El estudio analítico ha confirmado la solidez cualitativa del rebote (bounce). Las simulaciones numéricas han mostrado que esta solidez es también cuantitativa. Además, este análisis numérico ha demostrado que las amplitudes de las inhomogeneidades no cambian estadísiticamente en el proceso de rebote, excepto cuando son pequeñas, caso en el que parecen ser incrementadas por un tipo de mecanismo amplificador. Este mecanismo podría explicar la amplitud relativamente grande de las fluctuaciones primordiales si se confirmara en modelos cosmológicos más realistas.

En sistemas descritos por campos como el anterior, que poseen un número infinito de grados de libertad, un problema grave son las ambigüedades que se encuentran en el proceso de cuantización, que afectan al resultado final en la teoría cuántica. En el caso de una cuantización de Fock, donde se puede alcanzar un concepto de partícula (al menos hasta cierto punto), una parte importante de estas ambigüedades son las que surgen en la elección de una representación cuántica. Este problema se encuentra en teoría cuántica de campos estándar en espaciotiempos curvos, pero también en el caso de la cuantización de las inhomogeneidades dentro del esquema híbrido que hemos propuesto en el marco de la CCL. En situaciones estacionarias se sabe que criterios de simetría o de energía seleccionan una cuantización de Fock única. Nosotros, destacablemente, hemos sido capaces de probar recientemente que, incluso en escenarios no estacionarios, es posible elegir una única cuantización de Fock introduciendo criterios de a) invariancia del vacío bajo las simetrías de las ecuaciones de campo, y b) unitariedad en la evolución dinámica (respecto a un tiempo emergente relacionado con los elementos de área o volumen). Esta unicidad proporciona una solidez considerable a los resultados de la cuantización y a sus predicciones físicas. Específicamente, los teoremas de unicidad alcanzados hasta ahora se aplican al caso de campos escalares en cualquier topología espacial compacta y en cualquier dimensión espacial igual o menor que tres. Las aplicaciones para la cuantización sin ambigüedad de perturbaciones en cosmología son casi inmediatas.

Otra línea de investigación que hemos desarrollado ha sido el análisis de la radiación de Hawking en un agujero negro percibida por diferentes observadores. El método se basa en la introducción de una temperatura efectiva que varía con el tiempo. En primer lugar introducimos un vacío no estacionario que simula el proceso de encendido de la radiación de Hawking en un espacio tiempo estacionario y después lo analizamos desde la perspectiva de observadores estáticos en posiciones radiales fijas, observadores en caída libre y observadores estáticos que posteriormente se liberan y caen libremente. Los observadores en caída libre no perciben un estado de vacío cuando cruzan el horizonte, sino que sienten una temperatura efectiva un poco más grande que la que sentía antes de empezar a caer. Este fenómeno se explica en término de un efecto Doppler en el momento de cruce del horizonte. Desde otra perspectiva, usamos el problema transplanckiano de la radiación de Hawking como guía en la búsqueda de un modelo para la evaporación de agujeros negros o de objetos similares. Hemos argumentado que existen solo tres posibles situaciones, dependiendo de si la noción clásica de horizonte se preserva ante la presencia de fenómenos de alta energía y de si los objetos astrofísicos oscuros y compactos que observamos tienen horizontes o no. Hemos visto que i) una teoría con señales superluminales de alta energía y horizontes aparentes provocaría grandes inestabilidades en términos astrofísicos y que ii) las pulsaciones estelares de objetos con tamaño muy próximo a su radio gravitatorio pueden dar lugar a emisión de Hawking.

Líneas de Investigación:

• Gravedad y Cosmología Cuántica de Lazos.
• Relatividad General Clásica y Cuántica.
• Métodos computacionales en Física Gravitacional.
• Análogos de agujeros negros en Materia Condensada.

Labor Investigadora

Gravedad Cuántica

Durante el año 2010 hemos continuado con nuestro trabajo sobre la entropía de agujeros negros en gravedad cuántica de lazos, con el objetivo de entender su comportamiento para áreas del horizonte pequeñas. En particular, hemos desarrollado diversos métodos estadísticos que son necesarios para obtener un suavizado del muy complejo espectro de degeneración de los agujeros negros (y su versión integrada que da lugar a la entropía). Las aproximaciones suaves así obtenidas pueden ser utilizadas con éxito para entender el comportamiento de la entropía para áreas grandes. La idea principal consiste en introducir funciones generatrices modificadas obtenidas a partir de las que se han usado con éxito para describir la entropía de los agujeros negros. Estas nuevas funciones están diseñadas para permitir la extracción de la información estadística pertinente (la media y la varianza de la distribución definida por los picos que aparecen en el espectro de degeneración). En la actualidad se ha logrado una comprensión prácticamente completa de la estructura de la entropía como función del área con estos métodos.

En cuanto a nuestro trabajo sobre la cuantización de reducciones de simetría de la relatividad general, hemos completado un artículo para la serie Living Reviews on Relativity sobre la cuantización de los modelos de midisuperspacio. Éstos describen reducciones de simetría de la relatividad general con un número infinito de grados de libertad físicos. En contraste con los modelos minisuperspacio más familiares, se trata de teorías de campo genuinas que, en muchos casos, conservan una invariancia residual bajo difeomorfismos. Por estas razones, este tipo de modelos constituyen un excelente banco de pruebas para probar técnicas de cuantización y desempeñan un papel central en el desarrollo actual de la gravedad y cosmología cuánticas de lazos. Tratándose de un trabajo de revisión, el artículo no proporciona nuevos resultados, sino que más bien da una visión global del campo que tiene en cuenta todos los enfoques sobre el tema. Éstos incluyen tanto los métodos geometrodinámicos más tradicionales como los inspirados en la gravedad cuántica de lazos.

En lo concerniente, específicamente, a la aplicación de las técnicas de cuantización de lazos a tales midisuperespacios, hemos continuado desarrollando la cuantización de las cosmologías de Gowdy que contienen ondas gravitatorias linealmente polarizadas. De hecho, hemos completado su cuantización usando un formalismo híbrido que combina una cuantización de lazos de los modos cero de la geometría con una cuantización de Fock de los modos que describen las inhomogeneidades del campo gravitatorio. Hemos implementado con éxito las nuevas prescripciones para una dinámica mejorada en cosmología cuántica de lazos, determinado la estructura de los sectores de superselección del modelo, probado que el problema de valores iniciales está bien puesto en la teoría cuántica, y encontrado el espacio de Hilbert de estados físicos. Además, hemos llevado a cabo un análisis numérico de la dinámica efectiva correspondiente, mostrando que la singularidad cosmológica (inicial) se evita y es reemplazada por un rebote cuántico. Es más, este escenario de rebote cuántico no se ve afectado cualitativamente por la presencia de inhomogeneidades. También hemos estudiado el comportamiento de los modos inhomogéneos en el proceso del rebote, mostrando que sus amplitudes se conservan estadísticamente, salvo cuando son pequeñas, caso en el que se ven amplificadas por el rebote. Éste es el primer estudio del comportamiento de las inhomogeneidades en un modelo cuantizado por completo, dentro del marco de la cosmología cuántica de lazos.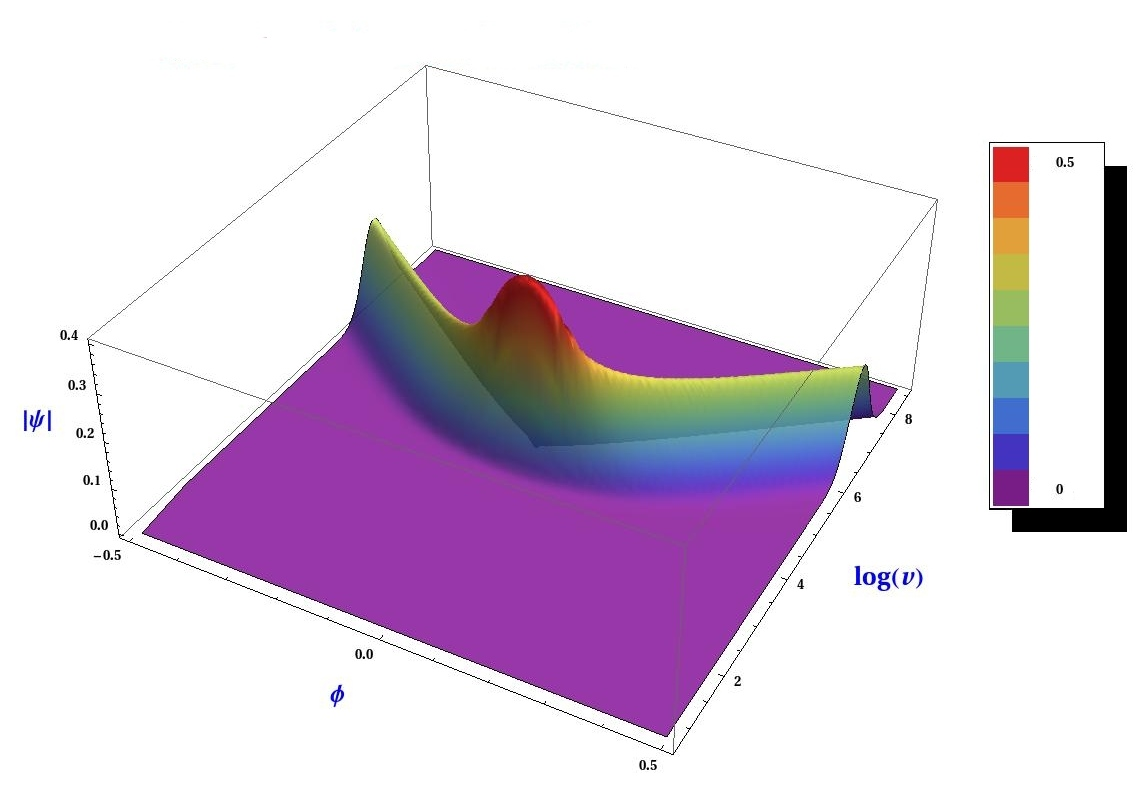

Rebote cuántico de la función de ondas del universo ψ para un espaciotiempo de Friedmann-Robertson-Walker con campo escalar ϕ. v corresponde al volumen del universo en unidades de Planck.

La elección de una cuantización de Fock en el formalismo híbrido propuesto se basa en ciertos teoremas de unicidad que hemos demostrado recientemente. Hemos probado que la selección, tanto de una descripción de campos (dentro de la familia de campos relacionados por transformaciones canónicas dependientes del tiempo) como de una representación de Fock para la misma, queda fijada, módulo equivalencia unitaria, si se requiere que el vacío sea invariante bajo las simetrías de las ecuaciones de campo y que la evolución dinámica sea unitaria (en la teoría deparametrizada). Estos teoremas eliminan las ambigüedades de teoría de campos en las predicciones cuánticas, por ejemplo, para campos inhomogéneos en fondos cosmológicos y para perturbaciones cosmológicas entorno a espaciotiempos de Friedmann-Robertson-Walker.

Otra línea de investigación que hemos desarrollado ha sido el estudio de análogos gravitatorios en física de material condensada. Hemos visto que las fluctuaciones de un condensado de Bose-Einstein se pueden describir tanto mediante la teoría de Bogoliubov como mediante una ecuación de Klein-Gordon modificada. Los conceptos de cuasipartícula que se derivan de ambos enfoques coinciden. En una configuración estacionaria que contenga un agujero negro acústico, existen varias elecciones posibles de un vacío regular, incluyendo una generalización regular del vacío de Boulware. La descripción de algunos fenómenos como la radiación de Hawking depende crucialmente de esta elección de vacío. En otro frente distinto, hemos determinado el grado de entrelazamiento de un sistema bipartito Alice-Rob (cuando Rob se halla en las proximidades de un agujero negro de Schwarzschild y Alice se halla cayendo libremente en él) como función de la distancia de Rob al horizonte y de la frecuencia. Todos los fenómenos interesantes ocurren en la vecindad del horizonte de sucesos y su presencia no degrada el entrelazamiento cuando Rob se halla en una zona muy alejada del agujero negro. Por otro lado, el vacío puede evolucionar en un estado entrelazado en un proceso dinámico de colapso. Hemos visto que este entrelazamiento podría alcanzar incluso un grado máximo para frecuencias bajas o para agujeros negros suficientemente pequeños. El colapso gravitatorio proporciona recursos de información cuántica entre los modos en el futuro asintótico (radiación de Hawking) y aquéllos que caen hacia el horizonte. También hemos visto que los fermiones son más sensibles que los bosones a esta generación de entrelazamiento.

• Física Teórica: Gravitación.
• Teoría de la Materia Condensada.

• Gravedad y Cosmología Cuántica de Lazos.
• Relatividad General Clásica y Cuántica.
• Métodos computacionales en Física Gravitacional.
• Análogos de agujeros negros en Materia Condensada.
• Sistemas mesoscópicos y fuertemente correlacionados.

• Física Teórica y Matemática
• Métodos computacionales.

Labor Investigadora

Cosmología Cuántica de Lazos

Durante 2009, el Grupo de Física Gravitacional ha continuado su labor investigadora en el campo de la Cosmología Cuántica de Lazos (Loop Quantum Cosmology). La investigación se ha desarrollado en tres direcciones principales: la consolidación de los fundamentos de la Cosmología Cuántica de Lazos, la extensión de los resultados de modelos homogéneos e isótropos a casos anisótropos, y la inclusión de inhomogeneidades para permitir el estudio de perturbaciones cosmológicas.

La Gravedad Cuántica de Lazos (Loop Quantum Gravity) ha surgido en años recientes como un sólido candidato para alcanzar una teoría cuántica no-perturbativa de la Relatividad General. Se trata de una teoría independiente de fondos (backgrounds), basada en una descripción del campo gravitatorio en términos de holonomías y flujos. Para discutir sus implicaciones físicas, se ha prestado mucha atención a la aplicación de las técnicas de cuantización de la Gravedad Cuántica de Lazos en modelos reducidos por simetría que poseen soluciones cosmológicas. Esta línea de investigación es lo que se ha llamado la Cosmología Cuántica de Lazos.

La mayoría de la actividad en este campo se ha centrado en el análisis de modelos simples, homogéneos e isótropos. En particular, el caso del universo plano de Friedmann-Robertson-Walker (homogéneo e isótropo) con un campo escalar es un modelo paradigmático en Cosmología Cuántica de Lazos. A pesar del papel prominente que este modelo ha desempeñado en el desarrollo de esta rama de la física, algunos aspectos de su cuantización requerían de una discusión más detallada. Estos aspectos incluían la resolución cinemática de la singularidad cosmológica de big bang, la identificación de sectores de superselección lo más simples posible, y una comprensión clara del límite Wheeler-DeWitt asociado con la teoría en esos sectores. Nosotros propusimos un operador alternativo para representar la ligadura hamiltoniana que resulta especialmente adecuado para tratar los puntos mencionados de forma satisfactoria. En particular, nuestra ligadura conduce a sectores simples de superselección para el volumen del universo, con soporte contenido en un semieje único de la recta real, y para el que las funciones básicas que contienen la información sobre la geometría poseen propiedades físicas óptimas. A saber: proporcionan una descripción de no-boundary (ausencia de contorno) entorno a la singularidad cosmológica y admiten un límite Wheeler-DeWitt bien definido en términos de ondas estacionarias. Ambas propiedades explican la presencia de un rebote (bounce) cuántico genérico que reemplaza la singularidad de big-bang a un nivel fundamental, en contraste con estudios previos donde se demostró la existencia del rebote sólo en regímenes concretos y centrándose en estados con un marcado comportamiento semiclásico.

Hemos mostrado también que la dinámica global de un universo homogéneo en Cosmología Cuántica de Lazos puede ser vista como un proceso de scattering. Esta imagen puede emplearse para construir un método versátil con el que verificar la conservación de las propiedades semiclásicas de los estados a través del rebote. El método se ha aplicado en detalle a dos ejemplos simples: un universo isótropo de Friedmann-Robertson-Walker, y el sector isótropo de un universo de tipo Bianchi I. En ambos casos, las dispersiones en el logaritmo del volumen y en el logaritmo del momento del campo escalar están relacionadas en el futuro y el pasado distantes. Esto conduce a una estricta conservación del comportamiento semiclásico.

Asimismo, hemos estudiado la auto-adjunción del operador de evolución correspondiente a un universo plano de Friedmann-Robertson-Walker con un campo escalar sin masa y una constante cosmológica positiva, descrito en el marco de la Cosmología Cuántica de Lazos. Se ha mostrado que, si la constante comológica es menor que un cierto valor, el operador admite muchas extensiones auto-adjuntas, cada una de ellas con un espectro puramente discreto. Por otra parte, cuando la constante cosmológica es mayor que el menor mencionado, el operador es esencialmente auto-adjunto, aunque el espacio de Hilbert físico no contiene ningún estado físicamente interesante en este caso.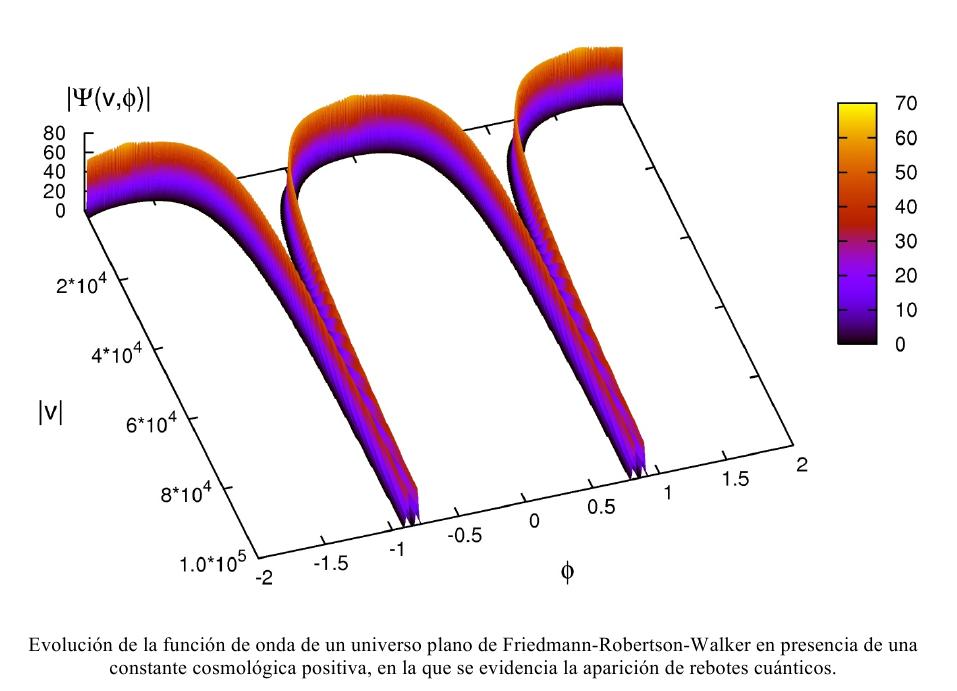

Hemos estudiado también en profundidad el modelo cosmológico anisótropo consistente en un universo de Bianchi I vacío, como un ejemplo para investigar el concepto de evolución física en Cosmología Cuántica de Lazos en ausencia del campo escalar sin masa que se usa frecuentemente como un reloj interno. Para extraer la dinámica del sistema cuando no está presente un reloj adecuado de ese tipo, hemos empleado diferentes construcciones de familias de observables parciales relacionados de manera unitaria. Estos observables están parametrizados, respectivamente, por una de las componentes de la tríada densitizada, o por su momento canónicamente conjugado; cada uno de ellos con su papel de parámetro de evolución. Aprovechando las propiedades del modelo considerado, hemos investigado en detalle los dominios de aplicabilidad de las construcciones introducidas. En ambos casos los observables poseen una interpretación nítida sólo en un sentido aproximado. Sin embargo, mientras que en el primer caso dicha interpretación es razonablemente aceptable tan sólo en una porción de la evolución del universo, en el segundo case permanece válida durante toda la evolución. Hemos usado estas familias de observables para describir la evolución del universo de Bianchi I. Nuestro análisis confirma la solidez de la predicción de los rebotes, también en ausencia de materia, así como la conservación de las propiedades semiclásicas a través de esos rebotes.

Además, como un paso necesario hacia la extracción de resultados realistas en Cosmología Cuántica de Lazos, hemos analizado las consecuencias físicas de la inclusión de inhomogeneidades. Hemos considerado la cuantización de un modelo gravitacional en vacío que posee grados de libertad local: las cosmologías de Gowdy con polarización lineal y con la topología espacial de un tres-toro. Hemos llevado a cabo una cuantización híbrida que combina técnicas de lazos y de Fock. Esta cuantización resuelve la singularidad cosmológica del big bang, y permite una definición rigurosa de las ligaduras cuánticas, así como la construcción de sus soluciones. Hemos determinado la estructura de Hilbert del espacio de estados físicos y, más aún, hemos recuperado a partir de ella una cuantización de Fock convencional para las inhomogeneidades.

La investigación teórica del grupo se ha visto complementada con trabajos en el frente numérico de la Relatividad General clásica y cuántica. Por ejemplo, hemos creado un paquete de álgebra computacional tensorial llamado xPert, para la construcción y manipulación de las ecuaciones de la teoría de perturbaciones métrica, alrededor de fondos (backgrounds) arbitrarios. Este paquete está basado en la compenetración de fórmulas combinatorias explícitas para el orden n-ésimo de las perturbaciones de tensores de curvatura y sus cambios gauge, y del uso de técnicas altamente eficientes de canonicalización de índices, proporcionadas por el sistema tensorial subyacente xAct (también hecho por uno de nosotros) para Mathematica.

Asimismo, usando herramientas para manipulaciones simbólicas eficientes desarrolladas por nosotros, hemos presentado un formalismo general invariante gauge para estudiar perturbaciones de segundo orden radiativas arbitrarias en un agujero negro de Schwarzschild. En particular, hemos construido las ecuaciones de segundo orden de Zerilli y de Regge-Wheeler bajo la presencia de dos modos de primer orden cualesquiera, hemos reconstruido la métrica perturbada en términos de los escalares máster, y hemos calculado la energía irradiada al infinito nulo. Nuestros resultados permiten estudios sistemáticos de perturbaciones genéricas de segundo orden para el espaciotiempo de Schwarzschild. Entre éstos, citamos los estudios de acoplo modo-modo y de los efectos no lineales en la radiación gravitatoria, o de la geometría del horizonte de agujero negro.

En un frente diferente, hemos analizado el proceso de radiación de Hawking debido a configuraciones de colapso gravitatorio en presencia de modificaciones superluminales de las relaciones de dispersión. Con estas relaciones de dispersión superluminales, el horizonte se convierte de manera efectiva en un concepto dependiente de la frecuencia. En particular, a cada momento del colapso, existe una frecuencia crítica por encima de la cual no se experimenta ningún horizonte. Hemos mostrado que, como consecuencia, la radiación a tiempos tardíos sufre modificaciones severas, tanto cuantitativas como cualitativas, en comparación con la descripción estándar de Hawking. Concretamente, el espectro de radiación se vuelve dependiente del tiempo de medida, de la gravedad de superfice asociada a diferentes frecuencias, y de la frecuencia crítica. Aparecen modificaciones importantes incluso si la frecuencia crítica está considerablemente por encima de la escala de Planck.

Gravedad Cuántica

Uno de los problemas más importantes en gravedad cuántica es la identificación de los grados de libertad microscópicos que dan cuenta de la entropía de los agujeros negros. Si fuera posible describirlos de manera inambigua y pudiéramos contarlos, podríamos obtener directamente el valor de la entropía. La relación entre la entropía y el área viene dada por la famosa fórmula de Bekenstein y Hawking que nos dice que la entropía es un cuarto del área del horizonte (en las unidades apropiadas). Las principales teorías candidatas para describir el régimen cuántico de la gravitación -las teorías de cuerdas y la gravedad cuántica de lazos- dan cuenta de esta ley. En el caso de la gravedad cuántica de lazos este resultado ha sido conocido durante más de una década, sin embargo, se ha descubierto recientemente que la entropía de los agujeros negros microscópicos, de acuerdo con la descripción proporcionada por la gravedad cuántica de lazos, presenta un comportamiento inesperado que consiste en una modulación superpuesta al crecimiento lineal de la entropía con el área. Lograr una comprensión detallada de este fenómeno ha sido una de las líneas de investigación principales en las que nuestro grupo ha trabajado durante el año 2009. En este campo hemos desarrollado, en colaboración con científicos de Valencia y Varsovia, una serie de métodos basados en teoría de números y combinatoria que nos han permitido alcanzar una comprensión más profunda de este problema. Entre ellas las más útiles han sido la identificación de un conjunto de ecuaciones diofánticas que simplifican la resolución exacta de los problemas de conteo que se plantean y la introducción de funciones generatrices para la entropía. También hemos encontrado el modo de conectar estos resultados con los métodos estándar que hacen uso de la transformada de Laplace.

Los resultados que hemos obtenido son múltiples. En primer lugar hemos podido demostrar que la modulación observada en la entropía puede estar presente en el régimen macroscópico (aunque el comportamiento asintótico exacto aún no ha sido obtenido). Este resultado es consecuencia de la sutil forma en la que el comportamiento asintótico de la entropía está descrito por la integral (transformada de Laplace inversa) que expresa la entropía en función del área. Concretamente, la acumulación de las partes reales de los polos del integrando al valor que fija el crecimiento lineal de la entropía, es compatible con el comportamiento lineal dado por la ley de Bekenstein- Hawking, pero permite que exista una corrección periódica subdominante que podría explicar la estructura observada en la entropía de los agujeros negros microscópicos.

Hemos aprovechado estos métodos para calcular la entropía de los agujeros negros siguiendo definiciones alternativas a las usuales. En particular, hemos considerado una definición, distinta de la habitual, para el operador de área utilizado en la definición de la entropía. Como es bien sabido, en el caso de los horizontes aislados (en contraste con el caso correspondiente a superficie cerradas arbitrarias), es posible considerar otras definiciones para el área, [aunque hay que decir que la definición estándar, con el espectro habitual no equiespaciado, es la preferida]. Entre ellas hay una elección muy simple y natural que da lugar a un espectro equiespaciado. Esto tiene algunas consecuencias por lo que se refiere a la definición de la entropía. En una colaboración con Jerzy Lewandowski (Universidad de Varsovia), se han explorado las consecuencias físicas de la adopción de la definición modificada y hemos comprobado que el esperado comportamiento de la entropía está de hecho presente. Una característica notable de este trabajo es el hecho de que hemos sido capaces de obtener expresiones exactas (en forma cerrada) para la entropía y reproducir la ley de Bekenstein-Hawking. Por último, otra aplicación de nuestros métodos ha sido el cálculo de la entropía en el nuevo esquema presentado recientemente por Engle, Noui y Pérez, para definir la entropía de los agujeros negros en gravedad cuántica de lazos mediante una descripción en la que los grados de libertad en el horizonte de un agujero negro vienen dados por una teoría de Chern-Simons para el grupo SU(2).

Durante el año pasado, nuestro grupo ha continuado con su tradicional línea de trabajo sobre la cuantización de los modelos de midisuperespacio -en particular de los universos de Gowdy- tanto dentro de la teoría cuántica de campos habitual como de la gravedad cuántica de lazos. En este sentido, hemos dedicado algunos esfuerzos a desarrollar en detalle los aspectos referidos a la cuantización del oscilador armónico con frecuencia dependiente del tiempo que podrían ser exportados al estudio de los modelos Gowdy. Es importante señalar a este respecto que los modelos de Gowdy pueden ser considerados como teorías de campo descritas por una infinidad de osciladores de ese tipo. Los métodos utilizados en este análisis han sido múltiples y han ampliado considerablemente los desarrollados en trabajos previos. Apoyándonos en estos resultados se ha construido una representación de Schrödinger funcional que ha permitido abordar varios problemas; en particular, la definición de una dinámica unitaria y la existencia de estados semiclásicos.

La labor investigadora en física gravitacional se ha completado con las siguientes contribuciones:

• Gravedad Modificada: hemos profundizado en el estudio de teorías de gravedad modificada en el formalismo de Palatini para determinar la habilidad de dichas teorías para generar cosmologías no singulares. Hemos centrado nuestra atención en teorías del tipo f(R) en Universos Fridemann-Robertson-Walker. Hemos encontrado que las condiciones para la existencia de un rebote cosmológico son bastante genéricas, estando determinadas únicamente por la existencia de un cero en la derivada del lagrangiano f(R). De manera notable, hemos obtenido un lagrangiano f(R) que reproduce de manera exacta la dinámica efectiva de LQC con un campo escalar sin masa, lo que demuestra el potencial de estas teorías para capturar ciertos aspectos de la fenomenología de gravedad cuántica y motiva más investigación en esta dirección.

• Cosmología inflacionaria: hemos estudiado la generación de perturbaciones primordiales en un universo inflacionario de tipo slow-roll con un campo escalar. En espacio de momentos, las perturbaciones (gaussianas) están caracterizadas por una media nula y una varianza no nula. Sin embargo, de acuerdo con la literatura, la varianza en espacio de posiciones diverge en el ultravioleta. Hemos reconsiderado el cálculo de la varianza en espacio de posiciones usando métodos bien establecidos de renormalización en espacios curvos. Este procedimiento afecta las predicciones referentes a los espectros de potencias escalares y tensoriales para longitudes de onda observables hoy en día. En consecuencia, la huella de la inflación en las anisotropías del fondo de microondas se ve significativamente alterada con respecto a la predicción estándar. En particular, encontramos un cambio no trivial en la relación de consistencia que relaciona el cociente de amplitudes escalar y tensorial con los índices espectrales. La influencia del fondo primordial de ondas gravitatorias en el fondo de microondas puede que sea observable en el futuro próximo, lo que ofrece un test no trivial de nuestras nuevas predicciones.

• Agujeros negros: un aspecto molesto de la derivación de Hawking de la radiación de agujeros negros es la necesidad de invocar condiciones extremas para el campo cuántico que origina los cuantos emitidos. Se suele argumentar que la derivación requiere la estricta validez de la teoría de campos relativista hasta escalar de energía arbitrariamente altas (por encima de la escala de Planck). Usando las funciones de correlación del campo de materia, hemos demostrado que esto no es necesariamente así si el problema se plantea de manera covariante. Hemos encontrado que la radiación de Hawking es robusta bajo la introducción de una frecuencia de corte a la escala de Planck.

Propiedades Electrónicas de Grafeno

Durante el año 2009 hemos continuado con la investigación teórica de las propiedades electrónicas del grafeno, es decir, el material hecho de carbono de un solo átomo de espesor y con la coordinación hexagonal típica de las láminas de grafito. Desde su descubrimiento en 2004, la investigación del grafeno ha suscitado un interés creciente en la comunidad de la física de materia condensada, en tanto que el carácter genuinamente bidimensional del material le hace susceptible de tener propiedades no convencionales referidas a su comportamiento elástico, óptico y electrónico. Nuestra investigación se ha centrado en el análisis de las inestabilidades superconductoras del grafeno a alto nivel de dopado, así como en el estudio de los efectos de la curvatura de esta peculiar membrana metálica.

La investigación del estado fundamental del grafeno a alto dopaje se ha emprendido en colaboración con un importante grupo experimental del Lawrence Berkeley National Laboratory. Una de las observaciones fundamentales de este grupo había sido que, bajo condiciones apropiadas de dopado químico, el nivel de Fermi se puede ajustar en torno de una singularidad de Van Hove en la banda de conducción del material de carbono bidimensional. Se sabe que la densidad de estados divergente en este tipo de singularidad puede conducir a diferentes tipos de inestabilidades en el líquido de electrones en dos dimensiones. En nuestro caso, hemos modelado la geometría específica de los puntos de silla extendidos que aparecen en la banda de conducción del grafeno, y que tienden a desarrollar valles alargados con dispersión casi plana siguiendo la frontera de la zona de Brillouin. Este carácter extendido de la singularidad tenía sólo precedente en la observación de la dispersión de ciertos superconductores de alta temperatura crítica. Nuestro análisis teórico ha mostrado de hecho que la superconductividad es una de las inestabilidades electrónicas que pueden aparecer cuando el grafeno está en torno de la singularidad de Van Hove de la banda de conducción. Esta conclusión se ha alcanzado mediante el cálculo del vértice BCS convenientemente vestido en el marco de la "random-phase approximation", y la posterior determinación de los acoplos e-e renormalizados en las diferentes representaciones del grupo de simetría puntual. Cerca de la singularidad de Van Hove, la fuerte modulación de la densidad de estados a lo largo de la línea de Fermi conduce siempre a la existencia de un acoplo negativo, que genera la inestabilidad superconductora a temperatura suficientemente baja. Hemos completado este análisis buscando también una posible inestabilidad magnética en el sistema, que podría surgir como consecuencia de la gran densidad de estados en torno de la singularidad de Van Hove. A tal fin, hemos calculado la susceptibilidad magnética en función de la temperatura para comparar su divergencia con respecto a la intensidad de la inestabilidad superconductora, encontrando que esta última prevalece en todo el rango de valores relevantes de la repulsión de Coulomb y del potencial químico alrededor de la singularidad de Van Hove. En combinación con la contribución experimental de la colaboración, nuestros resultados han permitido así apoyar la idea de que el grafeno altamente dopado puede entrar en una fase donde la superconductividad esté mediada por un mecanismo electrónico, siempre que el dopado alcance el nivel de la singularidad de Van Hove y que la simetría de la red se preserve, es decir, que los átomos dopantes no introduzcan nuevos estados cerca de la singularidad que puedan romper la estructura de bandas original.

Por otra parte, hemos estudiado los efectos de fuerte curvatura en el grafeno, continuando con nuestra investigación de las uniones entre grafeno y nanotubos de carbono. A este respecto, es muy prometedor que estas estructuras híbridas hayan sido ya fabricadas en los laboratorios Fujitsu, mientras que es también concebible que puentes entre dos hojas de grafeno se puedan construir a partir de las conocidas bicapas de grafeno. Nuestro análisis teórico se ha centrado en la geometría de puentes de grafeno en los que un nanotubo de carbono muy corto conecta las dos láminas, introduciendo 12 defectos heptagonales para curvar la red hexagonal de átomos de carbono. Tomando uniones de longitud muy pequeña en comparación con el radio del nanotubo, hemos desarrollado una teoría efectiva de fermiones de Dirac para describir las propiedades electrónicas de baja energía de estas uniones bicapa en el límite del continuo. En esta construcción, hemos incluido de forma apropiada el efecto que los anillos heptagonales inducen en los campos de Dirac representativos de las excitaciones electrónicas de baja energía. Esta acción se ha simulado anclando una línea de flujo magnético ficticio en cada defecto topológico, siguiendo el mismo procedimiento aplicado tiempo atrás en el caso de las redes de fullerenos. Los puentes entre hojas de grafeno representan de hecho una situación que puede considerarse en cierto modo dual al caso de los fullerenos, en tanto que los 12 anillos pentagonales en estas redes cerradas juegan un papel opuesto al de los defectos heptagonales en el puente. Hemos encontrado en particular que, cuando el flujo gauge efectivo de los defectos topológicos se hace máximo, los modos de energía cero de la ecuación de Dirac se agrupan en dos tripletes, que pueden considerarse como la contrapartida de los dos tripletes de modos cero que surgen en el límite continuo de fullerenos esféricos gigantes. Adicionalmente, hemos investigado los espectros de estas uniones bicapa llevando a cabo la diagonalización numérica de hamiltonianos de enlace fuerte en redes muy extensas con la geometría de tales puentes de grafeno. De esta manera, hemos demostrado la correspondencia entre el número de estados electrónicos localizados observados en el cálculo numérico y el flujo gauge efectivo predicho en el límite continuo. Hemos concluido así que los puentes de grafeno pueden ser descritos consistentemente por medio de una teoría efectiva de dos fermiones de Dirac en la correspondiente geometría curva, abriendo así la posibilidad de usar el material real de carbono para experimentar con la interacción entre la curvatura y los campos de Dirac. Es por tanto razonable pensar que el estudio de estos sistemas de materia condensada pueda permitir la investigación de efectos gravitatorios relevantes ligados al carácter de tipo Dirac de las cuasipartículas electrónicas, que de otro modo sólo serían accesibles a energías mucho mayores típicas de los fenómenos astrofísicos.

• Física Teórica: Gravitación.
  • Relatividad General Clásica y Cuántica.
  • Gravedad y Cosmología Cuántica de Lazos.
  • Métodos computacionales en Física Gravitacional.
  • Agujeros negros y análogos en Materia Condensada.
• Teoría de la Materia Condensada.
  • Sistemas de electrones fuertemente correlacionados.

Resumen

Gravitación

Durante el año 2007 se ha continuado desarrollando líneas ya tradicionales del Grupo de Física Gravitacional como son la cuantización de modelos cosmológicos de Relatividad General con infinitos grados de libertad correspondientes a inhomogeneidades, el estudio de la emergencia de escalas invariantes en Gravedad Cuántica y de sus posibles consecuencias para la existencia de límites de resolución espaciotemporal, o el estudio de análogos de agujeros negros en Física de la Materia Condensada.

En lo referente a cuantización de modelos cosmológicos obtenidos en Relatividad General por la imposición de simetrías, hemos estudiado en detalle el caso de las cosmologías de Gowdy con la topología de un tres-toro y con ondas gravitatorias linealmente polarizadas. Éste es un modelo arquetípico de soluciones cosmológicas con secciones espaciales compactas y que contienen grados de libertad locales correspondientes a las inhomogeneidades asociadas a ondas gravitatorias. Dichas cosmologías describen universos en expansión que, de forma genérica, comienzan en una singularidad inicial de tipo “big-bang”. En trabajos anteriores, habíamos demostrado que es posible alcanzar una teoría cuántica consistente para describir este modelo cosmológico a partir de técnicas propias de Teoría Cuántica de Campos en espacios curvos. Esta consistencia incluye la implementación de la dinámica del sistema (una vez fijado el gauge temporal convenientemente) mediante una transformación cuántica unitaria, compatible con la interpretación probabilística convencional de la Mecánica Cuántica. En dicha teoría cuántica, se adopta una representación de Fock para el campo escalar que contiene los grados de libertad locales asociados a las ondas gravitatorias. Esta cuantización es la primera descripción cuántica satisfactoria en la literatura de un modelo cosmológico con inhomogeneidades. Estos resultados se han complementado con la construcción de la representación de Schrödinger para el sistema. Hemos demostrado que esta descripción funcional es equivalente a la de Fock y mostrado cómo la evolución viene dada por una transformación unitaria en este contexto.

Asimismo, hemos completado estudios anteriores encaminados a probar que la teoría cuántica construida es la única físicamente aceptable. Hemos conseguido demostrar que, si se exige que la evolución del sistema y una simetría homogénea remanente en el mismo (que es la única simetría gauge del modelo) sean implementadas en la teoría cuántica como transformaciones unitarias, tanto la elección de campo fundamental para describir los grados de libertad locales de estas cosmologías como la cuantización de Fock que se adopta para ese campo son en realidad las únicas posibles, salvo por equivalencias unitarias que no alteran los resultados físicos. Este resultado es realmente llamativo, y proporciona una enorme solidez a las conclusiones derivadas de la cuantización del sistema. Es más, no existen precedentes en la literatura de teoremas de unicidad de este tipo para Teoría de Campos en espacios curvos con dependencia temporal.

Aún más, prosiguiendo con el estudio de estas cosmologías de Gowdy, hemos conseguido extender la cuantización al sistema sin fijación completa del gauge temporal y reemplazando las técnicas de cuantización de Teoría de Campos por las de Gravedad de Lazos. Para los estados físicos, esta cuantización conduce a la descripción ya construida de los grados de libertad inhomogéneos en términos de una representación de Fock, pero modifica el tratamiento de la evolución del sistema (ya que la variable de tiempo interno no se identifica ahora con una coordenada). De esta forma, la singularidad cosmológica inicial resulta ser evitada en la teoría cuántica, como se había comprobado ya que sucede para modelos de universos homogéneos en Cosmología Cuántica de Lazos. Por último y dentro del contexto de las reducciones de simetría se ha comenzado a explorar los aspectos clásicos y cuánticos asociados con las otras topologías posibles para modelos de Gowdy compactos: el producto de la esfera bidimensional por el círculo y la tres-esfera. Éste es un problema interesante porque permite explorar en un modelo exactamente resoluble cuál es la influencia de la topología tanto sobre aspectos físicos (asociados con la presencia de singularidades iniciales y finales) como matemáticos. En lo referente a este último aspecto es destacable el hecho de que la estructura de las ligaduras presentes en el modelo obtenido tras una deparametrización (similar a la empleada para el caso del tres-toro) es distinta a la habitual. Esto es debido en primer lugar a la aparición de las llamadas ligaduras polares, que tienen su origen en las condiciones de regularidad que es necesario imponer para tener en cuenta la presencia de puntos fijos (centros de rotación) de las transformaciones de simetría generadas por los campos de Killing. Por otra parte, cuando se fija el gauge no queda ninguna simetría residual (al contrario de lo que sucede en el caso del tres-toro) por lo que la formulación final del modelo resultante como sistema dependiente del tiempo es, en cierto sentido, más sencilla que las encontradas para las topologías estudiadas anteriormente. Un último comentario referente a este punto es el hecho de que todo el estudio se ha realizado para modelos de Gowdy acoplados a campos escalares sin masa utilizando las ideas que fueron introducidas con éxito para el acoplo de materia con ondas de Einstein-Rosen. Durante el año 2007 se completó también la cuantización de estos modelos. En particular se han identificado --y resuelto-- los problemas asociados con la dinámica cuántica utilizando técnicas geométricas.

Uno de los problemas cruciales de la gravedad cuántica es la comprensión detallada del límite semiclásico de la teoría. Como es bien sabido, éste es un problema resuelto y bien entendido para teorías libres ya que se basa en la extensión de la definición de los estados coherentes del oscilador armónico a sistemas que constan esencialmente de un número infinito de osciladores. En el caso de teorías en interacción el problema es mucho más difícil de tratar. De hecho, ni siquiera para sistemas con un número finito de grados de libertad, distintos del oscilador armónico, se conocen estados que tengan todas las buenas propiedades de los conocidos estados coherentes. Dentro del esquema teórico proporcionado por las reducciones de simetría de Relatividad General es posible plantearse estos problemas en situaciones lo suficientemente simples como para permitir un tratamiento exacto. En particular las ondas de Einstein-Rosen, que pueden ser descritas mediante un hamiltoniano que es una función sencilla del correspondiente a una teoría libre, son especialmente útiles para discutir este tipo de cuestiones. Hemos obtenido un resultado sencillo pero muy relevante en este contexto: la demostración de que es imposible construir estados que se comporten como los estados coherentes habituales incluso en un ejemplo tan sencillo como es un hamiltoniano que dependa funcionalmente de uno libre.

En lo referente al estudio de límites de resolución espacial y temporal debidos a la presencia conjunta de efectos cuánticos y gravitatorios, hemos profundizando en el análisis de las llamadas teorías de Relatividad Doblemente Especial, en las que las leyes de dispersión usuales se ven modificadas para permitir la existencia de una escala invariante de energía o momento (por ejemplo, la escala de Planck). Para implementar estas teorías en el espacio de posiciones existen diferentes propuestas. Un conjunto de ellas, que incluye una propuesta sugerida por nuestro Grupo, se basa en efectuar una implementación canónica en el espacio de fases. Esta implementación conduce a una geometría que depende directamente de la energía y momento del sistema. Nosotros hemos estudiado la relación entre todas las implementaciones canónicas de teorías de Relatividad Doblemente Especial que han aparecido en la literatura, y hemos podido demostrar que todas ellas son en realidad equivalentes.

Finalmente, para discutir el comportamiento de la incertidumbre temporal en Gravedad Cuántica, hemos analizado agujeros negros de tipo Schwarzschild-anti-de Sitter con posible contenido de radiación gravitatoria entre el horizonte y la región asintótica. Hemos utilizado el formalismo de horizontes aislados para estudiar con detalle las consecuencias de una redefinición no lineal de la masa de un agujero negro. El formalismo de horizontes aislados es un formalismo cuasilocal desarrollado para describir agujeros negros en equilibrio. En este formalismo, las posibles transformaciones hamiltonianas en el espacio de soluciones pueden identificarse con las elecciones aceptables de su función de masa (esto es, su energía). En presencia de escalas fundamentales, o incluso de la escala proporcionada por la constante cosmológica, distintas funciones de masa pueden entenderse como el resultado de una modificación que incorpora efectos gravitatorios, por ejemplo respecto a un fondo de tipo Schwarzschild convencional. Para estos sistemas hemos demostrado que, en cualquier descripción cuántica perturbativa, surge una incertidumbre temporal estrictamente positiva debida a la escala de energía que introduce la constante cosmológica. Por contra, en un esquema de cuantización en el que los efectos de dicha escala se incluyan de manera no perturbativa, es posible alcanzar una resolución temporal tan grande como se desee. Al menos desde este punto de vista, la existencia de una incertidumbre temporal mínima no es una característica general inevitable en escenarios de Gravedad Cuántica.

Simulación de la deformación de los conos de luz en torno al horizonte de un agujero negro.

En los temas de análogos de agujeros negros en Física de la Materia Condensada, hemos examinado el comportamiento de condensados de Bose-Einstein con una densidad y perfil de velocidad que permiten la presencia de un horizonte acústico. En particular, hemos llevado a cabo un análisis de los modos cuasinormales de configuraciones análogas a agujeros negros en esta clase de condensados. En este análisis, hemos usado la relación de dispersión de Bogoliubov completa, y no la mera aproximación hidrodinámica o geométrica para la descripción del horizonte. Hemos restringido nuestro estudio a flujos unidimensionales en condensados con discontinuidades de tipo escalón. Para este caso, hemos demostrado que no existen modos cuasinormales en la aproximación hidrodinámica. Sin embargo, la relación de dispersión completa sí que permite la existencia de dichos modos. En contra de lo que se podría esperar inicialmente, el espectro de tales modos cuasinormales resulta ser continuo en vez de discreto.

Métodos computacionales en Física Gravitacional.

La Relatividad General de Einstein es una teoría geométrica del espaciotiempo gobernada por complicadas ecuaciones no lineales en derivadas parciales. Sólo en casos simplificados de muy alta simetría es posible desentrañar su contenido mediante lápiz y papel, por lo que el uso de técnicas computacionales se ha vuelto ahora indispensable para abordar problemas genéricos de interés astrofísico. Hay tres grupos de técnicas posibles: cálculo numérico, cálculo algebraico y desarrollos perturbativos. Nuestro Grupo utiliza todas ellas en diversos problemas y desarrolla herramientas específicas para su uso eficiente y sistemático. En particular durante el año 2007 hemos avanzado en los temas que describimos a continuación.

Nuestras técnicas y programas de cálculo algebraico tensorial eficiente nos han permitido resolver de forma práctica el problema clásico de las relaciones entre los invariantes escalares del tensor de Riemann, un problema al que se han dedicado específicamente varias docenas de artículos en las últimas décadas. Se trata de construir una base de monomios escalares del tensor de Riemann, y algoritmos capaces de expandir el resto de escalares como polinomios en aquéllos de la base. Estas relaciones son relevantes a la hora de analizar el problema de la renormalización de la gravedad de Einstein, o las múltiples generalizaciones de la Relatividad General propuestas actualmente, entre otros. Nuestros algoritmos son completamente nuevos y se basan en una combinación de computación en tiempo real de las partes del cálculo que pueden realizarse rápidamente, y la consulta de una base de datos que también hemos construido para aquellas otras partes que no pueden tratarse eficientemente. Esos algoritmos y la base de datos han sido codificados en el paquete Invar, distribuido como software libre. A diferencia de los métodos que se habían aplicado anteriormente a este problema, fuertemente adaptados a dimensión cuatro con signatura Lorentziana, nuestros algoritmos son válidos en cualquier caso, y fácilmente generalizables a cualquier otro tensor.

Mediante esas mismas técnicas de cálculo tensorial hemos completado nuestro formalismo general de perturbaciones de orden arbitrario alrededor de la simetría esférica, especialmente diseñado para estudiar problemas de generación de radiación gravitatoria en fenómenos dinámicos aproximadamente esféricos, como el colapso gravitatorio de una estrella rotante. Concretamente hemos construido un conjunto de variables perturbativas que poseen la importante propiedad de ser invariantes gauge, lo cual permite extraer con mayor facilidad el contenido físico de esas variables. Para ello, ha sido necesario analizar los diversos conceptos de invariancia gauge presentes en la literatura, estudiando su relación, y escoger cuál de ellos era el más conveniente y flexible para nuestros propósitos.

En tercer lugar, hemos continuado nuestro estudio general de la fenomenología de colapso gravitatorio crítico mediante simulaciones numéricas. Se trata de preparar adecuadamente una distribución inicial de materia que, al colapsar bajo la acción de su propia gravedad, forme un agujero negro muy pequeño, y en el límite de ajuste infinito una singularidad desnuda. La existencia de este tipo de fenómeno tiene profundas consecuencias en Relatividad General porque permite la generación de zonas del espacio en las que la curvatura crece sin límite sin estar rodeadas por un horizonte de sucesos. Esto supone una de las mejores vías de acceso al régimen cuántico de la gravedad. Nuestro trabajo este año se ha concentrado en la recopilación y sistematización de todos los resultados producidos en este campo desde su comienzo en 1992, lo que ha dado lugar a la publicación de un review en una revista especializada en artículos de revisión en Relatividad.

Propiedades electrónicas de materiales de carbono de baja dimensionalidad.

Desde el descubrimiento en 2004 de un nuevo material de carbono, consistente en láminas individuales de espesor atómico, se ha generado gran interés por el estudio de dicho agregado puramente bidimensional, denominado genéricamente como grafeno. Desde un punto de vista experimental, las hojas de carbono han mostrado ya un número de propiedades notables, entre las que se cuentan la cuantización anómala del efecto Hall y la existencia de un valor mínimo de la conductividad en el sistema sin dopar. Gran parte de las peculiaridades observadas en el material tienen su origen en una dinámica de las cuasipartículas gobernada por una ecuación de Dirac sin masa, que conduce a la aparición de un número cuántico adicional de pseudoespín en el espectro electrónico. Recientemente, ha habido experimentos donde se han medido las propiedades de transporte del grafeno cuando éste es contactado con electrodos superconductores. Así, se han podido observar supercorrientes fluyendo a través de la hoja de carbono, por debajo de la temperatura crítica de los electrodos.

En nuestra investigación teórica, hemos adoptado el tratamiento estadístico de la teoría de muchos cuerpos para entender el comportamiento de las uniones Josephson fabricadas con grafeno. Así, hemos descrito la aparición de las supercorrientes a partir de la transmisión por efecto túnel y propagación de pares de Cooper en la parte de grafeno de la unión, con el propósito de investigar la dependencia de las corrientes críticas en variables tales como la distancia entre contactos superconductores, la temperatura y el nivel de dopado. Hemos demostrado que las supercorrientes tienen una tendencia natural a decaer en el grafeno, siguiendo en general una ley de potencias como función de la distancia L entre los contactos superconductores. Este desvanecimiento es particularmente fuerte en el grafeno sin dopar, como consecuencia de la nula densidad de estados en el punto de neutralidad de carga. Hemos determinado que las corrientes críticas siguen a temperatura cero una dependencia de tipo 1/L^3 como función de la distancia. A temperatura distinta de cero, se ha constatado la existencia de una longitud térmica (inversamente proporcional a la energía térmica) más allá de la cual las supercorrientes son todavía más fuertemente suprimidas, debido a la ruptura de los pares de Cooper por efectos estadísticos.

Por otra parte, se ha tenido en cuenta la forma en que los efectos estadísticos de muchos cuerpos pueden potenciar las corrientes críticas, en este caso por medio del desplazamiento del nivel de Fermi fuera del punto de neutralidad de carga. Esta situación se puede describir en nuestro marco teórico introduciendo un potencial químico µ distinto de cero. Hemos visto que, induciendo de esta manera una densidad de estados finita en el nivel de Fermi, las corrientes críticas se ven potenciadas más allá de una nueva escala de longitud, inversamente proporcional a µ. A partir de esta escala los efectos de la densidad de estados finita se hacen sentir, provocando la transición de la anterior ley de potencias a un comportamiento de tipo 1/L^2 como función de la distancia entre electrodos.

Nuestra formulación a partir de la teoría de muchos cuerpos ha puesto también en evidencia que la gran ventaja de las uniones Josephson con grafeno proviene de la casi nula influencia de los efectos de la interacción de Coulomb, a las temperaturas requeridas para medir las supercorrientes. Esto representa una diferencia notable con respecto a las uniones unidimensionales hechas con nanotubos de carbono, donde la interacción electrónica repulsiva induce una fuerte supresión de la densidad de estados en el nivel de Fermi, con el consiguiente reflejo en el desvanecimiento de las supercorrientes. Por el contrario, en el grafeno bidimensional se constata la progresiva disminución de las correlaciones electrónicas a bajas energías, con una fuerte renormalización de la interacción de Coulomb que la convierte en prácticamente irrelevante a temperaturas del orden de 1 K. Nuestros resultados sirven en definitiva para clarificar el papel que los diferentes parámetros del sistema desempeñan en la determinación de las corrientes críticas en uniones Josephson de grafeno. Se ha puesto de manifiesto que es la conjunción entre los efectos de la temperatura y del dopado lo que determina los diferentes regímenes de la unión. Desde un punto de vista práctico, nuestra investigación revela que sería posible establecer supercorrientes por encima de la escala de 1 nA sobre distancias de varios cientos de nanómetros, para niveles convenientemente altos de dopado. Los resultados obtenidos pueden ser útiles en el diseño de experimentos, con el propósito de amplificar la magnitud de las corrientes críticas en dispositivos electrónicos a partir del grafeno.

• Física Teórica: Gravitación.
  • Relatividad General Clásica y Cuántica.
  • Métodos computacionales en Física Gravitacional.
  • Agujeros negros y análogos en Materia Condensada.
• Teoría de la Materia Condensada.
  • Sistemas de electrones fuertemente correlacionados.

Resumen

Gravitación

Durante el año 2006 se ha continuado trabajando con éxito en las líneas ya tradicionales del grupo en física gravitacional y cosmología: cuantización de modelos gravitatorios con inhomogeneidades obtenidos por reducción de simetría a partir de Relatividad General, estudio de la emergencia de escalas invariantes y de límites de resolución espaciotemporal en gravedad cuántica, formalismos de horizontes aislados y dinámicos, análogos de agujeros negros en materia condensada y aplicación de formalismos geométricos y de física matemática a la relatividad numérica.

En el área de la cosmología cuántica, nuestro trabajo se ha centrado en la aplicación de la teoría cuántica de campos a modelos en Relatividad General en los que la simetría reduce las complicaciones de la teoría general, pero aún así permite la existencia de grados de libertad locales en el campo gravitatorio. Hemos analizado en detalle el caso de las cosmologías de Gowdy, universos en expansión a partir de una singularidad inicial que contienen ondas gravitatorias con polarización lineal y cuya secciones espaciales son compactas. Como resultado de esta investigación, hemos construido una teoría cuántica consistente para describir dichos universos y tal que la evolución resulta venir dada por una transformación unitaria (que preserva la norma de los estados cuánticos). La cuantización se ha alcanzado empleando una representación de Fock para el campo escalar que describe los grados de libertad de las ondas gravitatorias. Ésta es la primera descripción cuántica consistente existente en la literatura de un modelo en Relatividad General con soluciones cosmológicas que contengan inhomogeneidades. Además, hemos demostrado que la cuantización propuesta es en realidad la única cuantización de Fock aceptable para el modelo de Gowdy (salvo equivalencias) si se exige que la dinámica cuántica sea unitaria y que cierta simetría homogénea que presenta el sistema se implemente como simetría cuántica. Este resultado da gran solidez a las posibles predicciones físicas de la cuantización construida, ya que no son consecuencia de elegir una descripción cuántica particular de entre un sinfín de teorías cuánticas para las cosmologías de Gowdy. Parte de la continuación de este trabajo consiste en explorar precisamente estas implicaciones y consecuencias físicas, entre ellas las relacionadas con el estudio de fluctuaciones (inhomogéneas) en cosmología.

Por otra parte se ha desarrollado un formalismo, basado en métodos utilizados en la cuantización de sistemas de osciladores armónicos con frecuencia dependiente del tiempo, que permite la obtención de los operadores de evolución unitaria para este tipo de reducciones de simetría, en particular los modelos de Gowdy, en forma analítica y cerrada. Aparte de proporcionar un marco alternativo en el que estudiar la unitariedad de la evolución cuántica en estos sistemas, la posibilidad de contar con expresiones analíticas permite plantearse la cuantización exacta mediante otro tipo de aproximaciones, en concreto las representaciones de tipo polimérico para campos escalares. Para ello será necesario obtener representaciones apropiadas para los operadores que aparecen como factores en el operador de evolución. Dado que éstos son exponenciales de objetos cuadráticos en los campos y sus momentos canónicamente conjugados parece ciertamente factible el análisis de las propiedades algebraicas de estos objetos y su posible representación como operadores con las propiedades adecuadas en un espacio de Hilbert.

En lo referente a la cuantización de las ondas de Einstein-Rosen, uno de los temas de trabajo tradicionales en el departamento se ha avanzado de manera notable en la obtención de predicciones de tipo físico para este sistema. En concreto se ha explotado la posibilidad de acoplar campos escalares sin masa para utilizarlos de manera efectiva como objetos de prueba con los que explorar la geometría cuantizada del modelo. En este sentido es destacable el análisis que se ha realizado sobre los propagadores -funciones de dos puntos del campo escalar- que admiten la interpretación de amplitudes de probabilidad de que un cuanto del campo creado en un suceso espacio-temporal concreto sea detectado en otro suceso distinto. La imagen así obtenida sobre los efectos de una cuantización del sistema gravitación-materia acoplado refuerza los resultados obtenidos mediante el análisis de la microcausalidad en este modelo y, en particular, los efectos cuánticos que aparecen en el eje de simetría. Quizá la herramienta más precisa que se ha introducido para llevar a cabo el tipo de análisis descrito anteriormente es la introducción de estados de tipo Newton-Wigner que permiten la introducción de funciones de onda normalizables que pueden ser interpretadas como amplitudes de probabilidad exactas de que partículas creadas a una cierta distancia del eje de simetría en un cierto instante de tiempo sean detectadas a otra distancia en un instante posterior. La posibilidad de analizar estas funciones de onda en gran detalle mediante el uso de las técnicas asintóticas introducidas en trabajos previos sobre este tema permite determinar bajo que circunstancias se puede obtener trayectorias espacio-temporales susceptibles de ser interpretadas como trayectorias clásicas del sistema. De esta manera podemos analizar en detalle como surgen las propiedades geométricas clásicas que caracterizan las geometrías pseudoriemannianas que caracterizan la relatividad general clásica.

En lo que respecta al estudio de límites de resolución temporal y espacial debidos a la presencia conjunta de efectos cuánticos y gravitatorios, nuestra investigación se ha centrado en las llamadas teorías de relatividad doblemente especial, en las que las leyes de dispersión usuales se ven modificadas para permitir la existencia de una escala invariante de energía o momento (por ejemplo, la escala de Planck). Para implementar estas teorías en el espacio de posiciones existen diferentes propuestas. Un conjunto de ellas se basa en efectuar una implementación canónica. Esta implementación conduce a una geometría que depende directamente de la energía y momento del sistema. Se llega así al formalismo llamado arco iris gravitatorio. Nosotros hemos demostrado que las diferentes propuestas de implementación canónica de relatividad doblemente especial aparecidas en la literatura son en realidad equivalentes. Además, hemos estudiado la alteración de las expresiones usuales del segundo principio generalizado de la termodinámica y de la temperatura y entropía de agujeros negros de Schwarzschild en el marco de arco iris gravitatorio. Hemos mostrado que la entropía deja de ser proporcional al área del agujero negro. Este hecho lleva a una definición de temperatura con un comportamiento muy diferente a la temperatura de Hawking convencional. La nueva temperatura no tiene por qué diverger cuando la masa del agujero negro se hace muy pequeña. Este resultado es importante porque sugiere que los agujeros negros podrían detener su evaporación o emplear un tiempo infinito en el proceso, abriendo nuevas posibilidades para la solución del problema de pérdida de información.

En lo concerniente a relatividad numérica, hemos generalizado a órdenes superiores el formalismo de Gerlach-Sengupta, elaborado inicialmente para el tratamiento a primer orden de las perturbaciones de un fondo esféricamente simétrico. Para ello se han tenido que generalizar los armónicos esféricos tensoriales de Gerlach-Sengupta a un número arbitrario de índices en la esfera. Utilizando técnicas de representaciones irreducibles del grupo de rotación se ha obtenido una fórmula cerrada para los productos de armónicos. El formalismo obtenido está optimizado para su implementación en un programa de cálculo tensorial simbólico, ya que dada la complejidad y longitud de las ecuaciones, se hace inevitable su uso. Nosotros lo hemos implementado en el paquete xTensor para Mathematica, del que somos autores. Como aplicación de las herramientas obtenidas se han calculado, por primera vez en la literatura, las fuentes completas para las ecuaciones de evolución a segundo orden perturbativo en el gauge de Regge-Wheeler. También se han obtenido las ecuaciones de conservación de energía-momento, comprobando, de esta manera, que las fuentes de las ecuaciones de evolución son consistentes con la identidad de Bianchi. La única propiedad que le falta a nuestro formalismo para que sea una generalización completa del de Gerlach y Sengupta a órdenes superiores es formularlo de manera invariante gauge. De este punto nos estamos ocupando actualmente.

Este año se ha completado nuestro estudio de las inestabilidades inherentes a las diversas formulaciones actualmente en uso en relatividad numérica. Estas inestabilidades tienen tres posibles orígenes: incorrectas condiciones de contorno, violaciones de las ligaduras y gauges mal puestos. En 2004 desarrollamos la técnica de condiciones de contorno constraint-preserving para resolver el primer problema; en 2005 introdujimos la técnica de constraint-damping para resolver el segundo (lo que permitió por primera vez una evolución estable de una binaria de agujeros negros), y este año 2006 hemos clasificado y analizado los diferentes gauges en uso en nuestra comunidad, señalando cuáles son problemáticos y sugiriendo cuáles son los mejores para la estabilidad de las evoluciones. Para ello también ha sido esencial el uso de nuestra herramienta xTensor de cálculo tensorial intensivo.

Finalmente, en temas de análogos de agujeros negros en física de la materia condensada, hemos examinado el comportamiento de condensados de Bose-Einstein con una densidad y perfil de velocidad que permiten la presencia de un horizonte acústico. En particular, hemos analizado las inestabilidades dinámicas y estudiado cómo se relacionan con la existencia real de horizontes acústicos. Para simplificar el estudio, hemos considerado perfiles unidimensionales que son uniformes a trozos, bien con una o dos discontinuidades de tipo escalón. Este caso idealizado contiene toda la información relevante para el análisis de perfiles de mayor complejidad.

Propiedades de transporte en materiales de carbono de baja dimensionalidad.

La investigación se ha centrado durante el año 2006 en el estudio de las propiedades electrónicas de láminas de grafito (grafeno) y nanotubos de carbono. La motivación por dicha investigación surge de la aparición de importantes resultados experimentales durante los últimos años, mostrando fenómenos notables en dichos materiales. Así, la posibilidad de separar láminas individuales de grafito ha permitido a varios grupos experimentales la medición de propiedades de transporte no convencionales, entre las que se encuentran la cuantización de la conductividad, que parece estar siempre por encima de un valor umbral, y la aparición de escalones típicos del efecto Hall cuántico en medidas de la magnetoresistencia, con una cuantización de la conductividad Hall en valores semienteros que es característica de los fermiones de Dirac.

Nuestro trabajo ha empezado por estudiar la formación de los niveles de Landau en redes de carbono en dos dimensiones, para investigar cómo los efectos del campo magnético se ven modificados por la curvatura de la red y, en particular, por el cambio de geometría en el caso de los nanotubos de carbono. Partiendo de modelos de enlace fuerte que describen los orbitales pi del carbono, la diagonalización del hamiltoniano correspondiente ha permitido encontrar la degeneración de los niveles, así como los estados de frontera que dan lugar a la cuantización de la conductividad en el efecto Hall. Estos resultados se han comparado con las teorías de campos efectivas obtenidas en el límite al continuo, a partir del acoplo entre el potencial vector electromagnético y los fermiones de Dirac que describen las cuasipartículas en el grafeno. De esta manera se ha llegado a una mejor comprensión de los efectos no convencionales que surgen de la invariancia de tipo relativista de las excitaciones electrónicas de baja energía en las redes de carbono.

En el caso de nanotubos de carbono de gran radio en campos magnéticos suficientemente intensos, se ha mostrado en particular que las propiedades de transporte están gobernadas por estados localizados en los flancos del nanotubo, que son responsables de la aparición de corrientes cuantizadas en la dirección longitudinal. Esto ha abierto la posibilidad de observar la cuantización de la conductividad Hall en nanotubos multicapa, donde típicamente la capa más externa es la única contactada por los electrodos en los experimentos de transporte. Se ha propuesto así un diseño experimental donde los escalones en la conductividad Hall se verían reflejados en las medidas del voltaje en la sección transversal del nanotubo, que podrían llevarse a cabo en particular mediante un microscopio de barrido por efecto túnel.

En otro apartado, se ha profundizado también en la investigación de la superconductividad de los nanotubos multicapa. A este respecto, ha despertado gran interés la observación de caídas abruptas en la resistencia de nanotubos multicapa por parte de un grupo experimental en Japón, que ha reportado temperaturas de transición del orden de 12K. En general, hemos podido constatar que la aparición de correlaciones superconductoras es posible en nanotubos donde la interacción de Coulomb se encuentra suficientemente apantallada. Esto sucede cuando hay un acoplo entre cargas de un número muy grande de canales de conducción, como en el caso de los nanotubos multicapa convenientemente dopados, donde pueden aparecer un número muy grande de sub-bandas al nivel de Fermi. Notablemente, nuestras predicciones parecen concordar con el hecho de que el mencionado grupo experimental haya observado caídas abruptas de la resistencia únicamente en muestras donde la mayor parte de las capas están contactadas por los electrodos.

En las investigaciones de superconductividad, hemos desarrollado un método que permite describir las inestabilidades electrónicas de nanotubos multicapa dopados. Nuestra técnica de cálculo reposa en la dependencia en la escala de energía de los diferentes procesos de interacción, y ha hecho posible el estudio de la transición del estado metálico normal de los nanotubos (líquido de Luttinger) a un estado superconductor a baja temperatura. Se ha establecido en particular que la coherencia tridimensional necesaria para éste último se abre a través de la transmisión de pares de Cooper por efecto túnel entre las diferentes capas de la estructura concéntrica del nanotubo multicapa. De esta manera, se ha construido el diagrama de fases en función del radio y del dopado de los nanotubos en dicha estructura. Se ha podido concluir que las predicciones dentro de nuestro marco teórico están de acuerdo con las observaciones experimentales, determinándose en última instancia las configuraciones óptimas que pueden permitir alcanzar mayores temperaturas de transición al estado superconductor.

Objetivos: Estudio de las inestabilidades electrónicas y superconductividad en nanotubos de carbono de pequeño diámetro y nanotubos multicapa.

• Física Teórica: Gravitación.
  • Relatividad General Clásica y Cuántica.
  • Métodos computacionales en Física Gravitacional.
  • Agujeros negros y análogos en Materia Condensada.
• Teoría de la Materia Condensada.
  • Propiedades electrónicas de nanotubos de carbono y grafito.

Resumen

Gravitación

Durante el año 2005 se ha continuado trabajando con éxito en las líneas ya tradicionales del grupo en gravitación y cosmología: cuantización de reducciones de simetría con dos vectores de Killing de relatividad general (ondas de Einstein-Rosen, modelos de Gowdy y de Schmidt), límites de resolución espaciotemporal, horizontes aislados y dinámicos, temas de relatividad numérica y análogos de agujeros negros en materia condensada. Por lo que respecta al primer punto el trabajo desarrollado para ondas de Einstein-Rosen se ha centrado preferentemente en el acoplo de campos de materia, específicamente, campos escalares sin masa. La incorporación de materia a estos modelos es una forma de enriquecerlos y aumentar su potencial físico, entre otras razones, porque así es posible contar con sondas externas que permitan extraer conclusiones de manera operacional sobre las consecuencias de haber cuantizado la geometría espacio-temporal. El hecho no trivial de que sea posible conseguirlo sin dejar de tener un modelo tratable de manera exacta en sus regímenes clásico y cuántico es un avance destacable en este campo que está siendo explotado en la actualidad.

En el área de la cosmología cuántica, nuestro trabajo se ha centrado en el llamado modelo de Gowdy T3, que describe soluciones cosmológicas con inhomogeneidades. Los intentos anteriores de otros grupos para obtener una descripción cuántica del modelo habían fracasado, porque conducían a una evolución no unitaria (con producción infinita de partículas en el vacío). Analizamos en detalle la dinámica del modelo y construimos una descripción cuántica en la que se solucionaban los problemas. Así, se ha conseguido por primera vez una cuantización consistente de un sistema cosmológico con inhomogeneidades (es decir, una teoría de cosmología cuántica de campos), compatible con la interpretación probabilística convencional de la mecánica cuántica. En la actualidad, estamos investigando las consecuencias de este formalismo cuántico.

En lo referente al estudio de los límites de resolución temporales y espaciales debidos a la presencia conjunta de efectos cuánticos y gravitatorios, nuestra investigación se ha centrado en las llamadas teorías de relatividad doblemente especial, en las que las leyes de dispersión usuales se ven modificadas para permitir la existencia de una escala invariante de energía o momento (por ejemplo, la escala de Planck). En este contexto, hemos mostrado que existen teorías donde se puede alcanzar una resolución temporal ilimitada cuando se realiza una descripción cuántica no perturbativa de las mediciones. Éste es el primer ejemplo contra la creencia de que es inevitable una incertidumbre espaciotemporal mínima en gravedad cuántica. Además, hemos conseguido identificar dominios de validez para distintos tipos de incertidumbres espaciotemporales que habían sido propuestas en la literatura.

Nuestro trabajo en Relatividad Numérica se ha centrado en dos frentes diferentes. Por un lado se ha continuado el análisis de las posibles formulaciones hiperbólicas de las ecuaciones de Einstein, intentando optimizar su eficiencia en las simulaciones numéricas. Una de las técnicas sugeridas por nosotros este año (llamada ``constraint damping´´) ha logrado estabilizar por primera vez la evolución de binarias de agujeros negros (recientes simulaciones de Frans Pretorius), lo cual ha supuesto un enorme avance en la resolución del problema más importante en Relatividad Numérica, y de gran relevancia en Astrofísica. Por otro lado, se ha seguido desarrollando el entorno de cálculo tensorial algebraico xTensor, con el que estamos actualmente abordando varios problemas que requieren cálculo muy intensivo, entre ellos teoría de perturbaciones de alto orden en Relatividad General, o el tratamiento de polinomios del tensor de curvatura.

Finalmente, en lo concerniente al tema de análogos de agujeros negros en física de la materia condensada, hemos examinado el comportamiento de condensados de Bose- Einstein con una densidad y perfil de velocidad que permiten la presencia de un horizonte acústico. En particular, hemos analizado las inestabilidades dinámicas y estudiado cómo se relacionan con la existencia real de horizontes acústicos. Para simplificar el estudio, hemos considerado perfiles unidimensionales que son uniformes a trozos, bien con una o dos discontinuidades de tipo escalón. Este caso idealizado contiene toda la información relevante para el análisis de perfiles de mayor complejidad.

Superconductividad en nanotubos de carbono y grafito.

Durante el año 2005 se ha investigado teóricamente la existencia de superconductividad en estructuras formadas por muchas capas concéntricas de nanotubos de carbono. Durante hace ya tiempo, los así llamados nanotubos multicapa han despertado gran interés debido a diversos efectos notables en sus propiedades de conducción (interferencia de ondas de electrón, transporte balístico, etc.). En este último año, un grupo de investigadores japoneses (J. Haruyama y colaboradores) ha realizado las primeras observaciones de lo que parecen ser transiciones a un estado superconductor en nanotubos multicapa, con temperaturas críticas en torno a 12 K, aproximadamente 25 veces por encima de las medidas en manojos de nanotubos. En estos experimentos los nanotubos han sido sintetizados en los poros de una matriz de óxido de aluminio, constatándose que la observación de la superconductividad resulta ser muy sensible al número de capas que son contactadas por los electrodos en los extremos de la matriz. Tomando como guía dichos experimentos, se ha procedido a la construcción de un marco teórico incorporando todos los factores relevantes para el transporte en los nanotubos multicapa. En particular, se ha considerado en detalle cada una de las componentes de la interacción electrón-electrón dentro de cada nanotubo individual, para discernir si el balance entre la repulsión de Coulomb y la interacción atractiva mediada por el intercambio de fonones puede ser favorable a la formación de pares de Cooper y desarrollo de correlaciones superconductoras. En el análisis teórico se ha distinguido entre lo que son propiedades de los nanotubos de carbono individuales y los efectos característicos que aparecen al considerar la interacción entre las diferentes capas concéntricas. En este sentido, el acoplo electrostático entre capas es un efecto importante pues tiende a apantallar de manera efectiva la repulsión de Coulomb dentro de cada nanotubo. Todavía más importante es que la transmisión de pares de Cooper por efecto túnel entre nanotubos vecinos permita abrir la coherencia tridimensional necesaria para la formación de todo estado superconductor. Teniendo en cuenta estos factores, se ha propuesto un modelo teórico que predice la aparición de transiciones superconductoras en nanotubos multicapa, para escalas de temperatura que son consistentes con las observadas experimentalmente. El estudio de dicho modelo ha permitido determinar el diagrama de fases del sistema electrónico, en función del número de capas metálicas de la estructura y del dopado.

El mismo marco teórico está siendo también empleado para describir el mecanismo de la superconductividad en grafito convenientemente dopado, entendiendo su estructura de láminas como el caso límite de un nanotubo multicapa cuando el radio se hace infinitamente grande. Se sabe desde hace ya tiempo que los compuestos intercalados de grafito, con átomos de elementos metálicos actuando como dopantes, son superconductores con temperaturas críticas que van desde la escala de 0.1 K hasta la de los 10 K. El hecho de que la escala superior de estas temperaturas sea comparable a la que se ha observado ahora en los nanotubos multicapa abre la perspectiva de que exista un marco común para la superconductividad de las diferentes estructuras de láminas de carbono. Otras investigaciones realizadas este último año han puesto de relieve que la curvatura de los nanotubos no juega un papel determinante en el desarrollo de las correlaciones superconductoras, y que en ello es más importante el número de canales (número de subbandas y de capas metálicas) que pueden estar abiertos para el transporte y deslocalización de los pares de Cooper. La investigación permitirá determinar, en definitiva, cuáles son los factores clave que posibilitan la formación del estado superconductor, con el propósito de indicar las condiciones experimentales óptimas para la consecución de mayores temperaturas de transición en el conjunto de los materiales de carbono.

• Física Teórica: Gravitación. Cuantización de ondas gravitatorias y agujeros negros. Durante el año 2004 se ha continuado con éxito el estudio de la cuantización de ondas gravitatorias con polarización lineal y simetría cilíndrica, conocidas como ondas de Einsten-Rosen. Se ha proseguido con el análisis de los valores en vacío de los conmutadores del campo que describe las ondas, mediante el que se había puesto de manifiesto la existencia de grandes efectos cuánticos. Concretamente, se ha demostrado la invalidez de su expansión en potencias de la constante gravitatoria, se ha descrito su comportamiento asintótico en distintos regímenes de interés físico, se ha analizado la influencia en este comportamiento de la presencia de un cutoff en el espacio de momentos y se ha constatado la falta de equivalencia entre los resultados de las cuantizaciones de Fock perturbativa y no-perturbativa. En particular, los vacíos de estas dos descripciones cuánticas no están relacionados mediante una serie de correcciones en la constante de interacción gravitatoria. Como consecuencia, no deben esperarse las mismas conclusiones físicas cuando los efectos cuánticos de las ondas se tienen en cuenta de forma global en la geometría desde un principio o cuando, por el contrario, se introducen mediante modificaciones sucesivas. Por otra parte, se ha comprobado que en el paso a la teoría cuántica las ondas gravitatorias cilíndricas con polarización general, que incluyen a las de Einstein-Rosen, constituyen un sistema que no es renormalizable en el sentido usual, aunque sí encaja en el esquema de asymptotic safety propuesto por Weinberg y considerado por Neidermaier en este contexto gravitatorio. Además, en teorías en las que la gravedad altera la expresión de la energía respecto a la usual en un fondo plano --como ocurre para estas ondas-- se ha mostrado que aparece una incertidumbre temporal mínima en los procesos de medición efectuados de acuerdo con la descripción cuántica perturbativa. Sin embargo, este límite de resolución temporal puede desaparecer, por lo general, en la teoría cuántica no-perturbativa. Otro tipo de problemas estudiado es la elaboración de un formalimo geométrico para caracterizar las membranas del espacio-tiempo que proporcionan los horizontes de los agujeros negros. A partir del formalismo de horizontes aislados propuesto por el Prof. Ashtekar, diseñado para describir horizontes gravitatorios en equilibrio, se han deducido condiciones de contorno adecuadas para afrontar la integración numérica de las ecuaciones elípticas que aparecen en el problema de valores iniciales para espacio-tiempos que contienen agujeros negros. Estas condiciones pueden ser aplicadas en relatividad numérica para obtener simulaciones con las que estudiar la evolución de ese tipo de sistemas, con la vista puesta en el problema de binarias de agujeros negros, de interés en astrofísica y en interferometría de ondas gravitatorias.
• Teoría de la Materia Condensada:Propiedades electrónicas de nanotubos de carbono. Durante el año 2004 se han estudiado las propiedades de los sistemas híbridos formados por la inserción de fullerenos en el interior de nanotubos de carbono. Los espectros electrónicos de dichos sistemas muestran peculiaridades que no se pueden explicar por la simple hibridación de los orbitales moleculares de fullerenos y nanotubos de carbono. Una de las características más relevantes en el caso de nanotubos semiconductores consiste en la aparición de una modulación en el gap del espectro, que conlleva una reducción notable de dicho gap en torno de la posición de los fullerenos. Para dar cuenta de dicho efecto se ha introducido un modelo para los estados electrónicos de baja energía del sistema, incorporando la interacción electrostática del nanotubo con la carga eléctrica de los fullerenos. Partiendo de la base de que la modulación del gap se ha observado en sistemas formados con metalofullerenos cargados, se ha propuesto un mecanismo por el que la reducción del gap tiene lugar por la formación de estados ligados, con niveles de energía por debajo del fondo de la banda de conducción. Los cálculos llevados a cabo han tenido en cuenta las propiedades de apantallamiento de la interacción dentro de la estructura de los nanotubos, concluyéndose que los estados ligados están localizados en una extensión espacial que es consistente con la de la modulación observada en los experimentos. El estudio realizado muestra que tal modulación debe ser sensible en general a la carga contenida en los fullerenos y a las propiedades de apantallamiento del substrato utilizado. Esto abre la posibilidad de controlar a voluntad la magnitud del gap en los nanotubos semiconductores, haciendo que los mencionados sistemas híbridos se sitúen como buenos candidatos para el diseño de dispositivos en electrónica molecular. En un estudio aparte, se han investigado también las propiedades de transporte por efecto túnel en estructuras con muchas capas de nanotubos concéntricos. Dichos sistemas han demostrado tener comportamientos de la conductancia que son consistentes con un decaimiento en forma de ley de potencias de la densidad de estados a baja energía, pero con un exponente que depende del valor del voltaje aplicado al electrodo del gate, con oscilaciones de período en torno a ~ 2 V. Para explicar tal fenómeno se ha partido de un modelo apropiado para describir las propiedades de escala anómalas debidas a la interacción electrónica, pero teniendo también en cuenta la naturaleza discreta del espectro electrónico como consecuencia de la cuantización de los niveles moleculares. Dicho carácter discreto aparece también a raíz de la energía necesaria para añadir un electrón de más en la geometría finita del nanotubo, dando lugar a las propiedades del régimen llamado de bloqueo de Coulomb. La descripción llevada a cabo puede así considerarse como una interpolación entre el régimen de alta temperatura, donde la conductancia muestra el mencionado comportamiento en forma de ley de potencias, y el régimen de bloqueo de Coulomb a baja temperatura, en el que la conductancia muestra oscilaciones bajo variaciones en el voltaje del gate que son un reflejo del carácter discreto de los niveles. Los resultados obtenidos dentro del marco teórico propuesto muestran que, en el régimen intermedio, la conductancia tiene todavía un comportamiento en forma de ley de potencias como función de la temperatura, pero con un exponente que depende de la posición del nivel de Fermi en el conjunto de niveles. Se ha encontrado que las estimaciones para el período de las oscilaciones en el exponente son consistentes con el valor del período observado en los experimentos, lo que, junto con el acuerdo con otros detalles en las curvas de la conductancia, muestra la plausibilidad de la descripción de un régimen intermedio entre el de bloqueo de Coulomb y el régimen de alta temperatura de los nanotubos de carbono.